题目内容
已知: 、
、 是坐标平面上的点,O是坐标原点.
是坐标平面上的点,O是坐标原点.
(Ⅰ)若点Q的坐标是 ,求
,求 的值;
的值;
(Ⅱ)设函数 ,求f(a)的值域.
,求f(a)的值域.
解:(Ⅰ)由已知条件,得 .…(3分)
.…(3分)
所以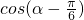 =cosαcos
=cosαcos +sinαsin
+sinαsin =-
=- ×
× +
+ ×
× =
=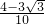 .…(6分)
.…(6分)
(Ⅱ) =cos
=cos cosα+sin
cosα+sin sinα=cos(α-
sinα=cos(α- ) …(9分)
) …(9分)
因为 ,则
,则 ,
,
∴ .
.
故f(α)的值域是 .…(12分)
.…(12分)
分析:(I)由已知条件,可得sinα和cosα的值,再结合两角差的余弦公式,可算出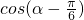 的值;
的值;
(II)根据平面向量数量积的坐标公式和两角差的余弦公式,可得f(α)=cos(α- ),再结合余弦函数的图象与性质,可得函数f(α)=的值域.
),再结合余弦函数的图象与性质,可得函数f(α)=的值域.
点评:本题以平面向量的数量积坐标运算为载体,着重考查了两角差的余弦公式和余弦函数的图象与性质等知识,属于基础题.
 .…(3分)
.…(3分)所以
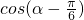 =cosαcos
=cosαcos +sinαsin
+sinαsin =-
=- ×
× +
+ ×
× =
=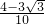 .…(6分)
.…(6分)(Ⅱ)
 =cos
=cos cosα+sin
cosα+sin sinα=cos(α-
sinα=cos(α- ) …(9分)
) …(9分)因为
 ,则
,则 ,
,∴
 .
.故f(α)的值域是
 .…(12分)
.…(12分)分析:(I)由已知条件,可得sinα和cosα的值,再结合两角差的余弦公式,可算出
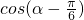 的值;
的值;(II)根据平面向量数量积的坐标公式和两角差的余弦公式,可得f(α)=cos(α-
 ),再结合余弦函数的图象与性质,可得函数f(α)=的值域.
),再结合余弦函数的图象与性质,可得函数f(α)=的值域.点评:本题以平面向量的数量积坐标运算为载体,着重考查了两角差的余弦公式和余弦函数的图象与性质等知识,属于基础题.

练习册系列答案
相关题目
在坐标平面上,圆C的圆心在原点且半径为2,已知直线L与圆C相交,则直线L与下列图形一定相交的是( )
| A、y=x2 | ||||
B、y=(
| ||||
| C、x2+y2=3 | ||||
D、
|
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B. 与圆C相交,则直线
与圆C相交,则直线 B.
B. C.
C. D.
D.