题目内容
【题目】在平面直角坐标系![]() 中,已知双曲线
中,已知双曲线![]() :
:![]() .
.
(1)设![]() 是
是![]() 的左焦点,
的左焦点,![]() 是
是![]() 右支上一点.若
右支上一点.若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)设斜率为1的直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 与圆
与圆![]() 相切,求证:
相切,求证:![]() ;
;
(3)设椭圆![]() :
:![]() .若
.若![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() ,求证:
,求证:![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.
【答案】(1) (2)证明见解析(3)证明见解析
(2)证明见解析(3)证明见解析
【解析】
(1)利用![]() ,建立方程,即可求
,建立方程,即可求![]() 点的坐标.
点的坐标.
(2)设直线![]() 的方程为
的方程为![]() ,通过直线
,通过直线![]() 与已知圆相切,得到
与已知圆相切,得到![]() ,通过求解
,通过求解![]() .证明
.证明![]() .
.
(3)当直线![]() 垂直
垂直![]() 轴时,直接求出
轴时,直接求出![]() 到直线
到直线![]() 的距离为
的距离为![]() .当直线
.当直线![]() 不垂直
不垂直![]() 轴时,设直线
轴时,设直线![]() 的方程为:
的方程为:![]() ,(显然
,(显然![]() ),推出直线
),推出直线![]() 的方程为
的方程为![]() ,求出
,求出![]() ,
,![]() ,设
,设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,通过
,通过![]() ,求出
,求出![]() .推出
.推出![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.
(1)左焦点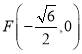 .
.
设![]() ,则
,则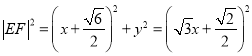 ,
,
由![]() 是右支上一点,知
是右支上一点,知![]() ,所以
,所以![]() ,得
,得![]() .
.
所以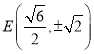 .
.
(2)证明:设直线![]() 的方程是
的方程是![]() .因直线与已知圆相切,
.因直线与已知圆相切,
故![]() ,即
,即![]() .
.
由![]() 与双曲线
与双曲线![]() :
:![]() 联立,得
联立,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
又![]() .
.
所以![]()
![]()
![]() .
.
故![]() .
.
(3)当直线![]() 垂直于
垂直于![]() 轴时,
轴时,
![]() ,
,![]() ,则
,则![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
当直线![]() 不垂直于
不垂直于![]() 轴时,
轴时,
设直线![]() 的方程为
的方程为![]() (显然
(显然![]() ),则直线
),则直线![]() 的方程为
的方程为![]() .
.
由![]() 与椭圆方程联立,得
与椭圆方程联立,得![]() ,
,![]() ,所以
,所以![]() .
.
同理![]() .
.
设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,因为
,因为![]() ,
,
所以 ,即
,即![]() .
.
综上,![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.

练习册系列答案
相关题目
【题目】某企业生产A产品的质量以其质量指标值衡量,质量指标值划分等级及产品售价如下表:
质量指标值m |
|
|
|
产品等级 | 等品 | 二等品 | 三等品 |
售价(每件) | 160元 | 140元 | 120元 |
从该企业生产的A产品中抽取100件作为样本,检测其质量指标值,得到下图的频率分布直方图.
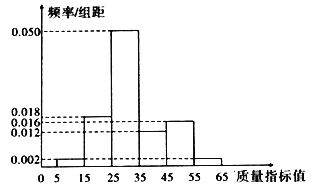
(1)根据频率分布直方图,求A产品质量指标值的中位数;
(2)用样本频率估计总体概率.现有一名顾客随机购买两件A产品,设其支付的费用为X元,求X的分布列及数学期望.