题目内容
设函数 (
(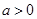 ).区间
).区间 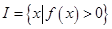 ,定义区间
,定义区间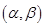 的长度为 b-a .
的长度为 b-a .
(1)求区间I的长度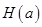 (用 a 表示);
(用 a 表示);
(2)若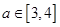 ,求
,求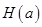 的最大值.
的最大值.
(1) (2)
(2)
解析试题分析:(1)对函数先进行因式分解,再利用一元二次不等式可解出解集,然后利用定义区间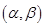 的长度为 b-a .可求出区间I。
的长度为 b-a .可求出区间I。
(2)由(1)已经得出 ,又
,又 分子分母同除以a再根据对勾函数的性质可得出它的最大值。
分子分母同除以a再根据对勾函数的性质可得出它的最大值。
试题解析:(1) 
 ,
, .
.  解集为
解集为 . 4分
. 4分
所以区间长度为 5分
5分
(2) 由(1)知, 7分
7分 在
在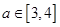 单调递增. 13分
单调递增. 13分
所以,当 时,I取最大值
时,I取最大值 14分
14分
(第二问解法不同但说理清晰严密即给满分)
考点:不等式的解法,定区间求最值。

练习册系列答案
相关题目
不等式 的解集为( )
的解集为( )
A.(﹣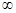 ,﹣2)∪(﹣1,+ ,﹣2)∪(﹣1,+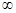 ) ) |
B.(﹣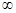 ,1)∪(2,+ ,1)∪(2,+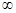 ) ) |
| C.(﹣2,﹣1) |
| D.(1,2) |
[2014·常州质检]已知f(x)=x+ -2(x<0),则f(x)有( )
-2(x<0),则f(x)有( )
| A.最大值为0 | B.最小值为0 |
| C.最大值为-4 | D.最小值为-4 |
 ”将
”将 从小到大排列是 .
从小到大排列是 .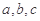 为三角形
为三角形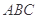 的三边,求证:
的三边,求证: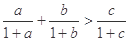
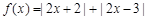 .
.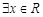 ,使得不等式
,使得不等式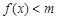 成立,求
成立,求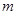 的取值范围;
的取值范围;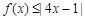 成立的
成立的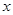 的取值范围.
的取值范围.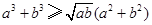 .
. .
.
 .
.