题目内容
数列{an}和数列{bn}(n∈N*)由下列条件确定:
(1)a1<0,b1>0;
(2)当k≥2时,ak与bk满足如下条件:当 ≥0时,ak=ak-1,bk=
≥0时,ak=ak-1,bk= ;当
;当 <0时,ak=
<0时,ak= ,bk=bk-1.
,bk=bk-1.
解答下列问题:
(Ⅰ)证明数列{ak-bk}是等比数列;
(Ⅱ)记数列{n(bk-an)}的前n项和为Sn,若已知当a>1时, =0,求
=0,求 .
.
(Ⅲ)m(n≥2)是满足b1>b2>…>bn的最大整数时,用a1,b1表示n满足的条件.
解:(Ⅰ)当 ≥0时,bk-ak=
≥0时,bk-ak= -ak-1=
-ak-1= (bk-1ak-1),
(bk-1ak-1),
当 <0时,bk-ak=bk-1-
<0时,bk-ak=bk-1- =
= (bk-1ak-1),
(bk-1ak-1),
所以不论哪种情况,都有bk-ak= (bk-1ak-1),又显然b1-a1>0,故数列{ak-bk}是等比数列(4分)
(bk-1ak-1),又显然b1-a1>0,故数列{ak-bk}是等比数列(4分)
(Ⅱ)由(Ⅰ)知,bn-an=(b1-a1)= ,故n(bn-an)=(b1-a1)•
,故n(bn-an)=(b1-a1)•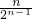 ,
,
Sn=(b1-a1)(1+ +
+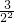 +…+
+…+ +
+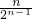 ),所以
),所以 Sn=(b1-a1)(1+
Sn=(b1-a1)(1+ +
+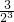 …+
…+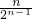 +
+ ),
),
所以 Sn=(b1-a1)(1+
Sn=(b1-a1)(1+ +
+ +…+
+…+ +
+ ),Sn=(b1-a1)[4(1-
),Sn=(b1-a1)[4(1- )-
)- ](7分)
](7分)
又当a>1时
 =0,
=0, Sn=4(b1-a1).(8分)
Sn=4(b1-a1).(8分)
(Ⅲ)当b1>b2>…>bn(n≥2)时,bk≠bk-1(2≤k≤n),由(2)知 <0不成立,
<0不成立,
故 ≥0,从而对于2≤k≤n,有ak=ak-1,bk=
≥0,从而对于2≤k≤n,有ak=ak-1,bk= ,于是an=an-1=…=a1,
,于是an=an-1=…=a1,
故bn=a1+(b1-a1) (10分)
(10分)
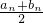 =
= {a1+[a1+(b1-a1)
{a1+[a1+(b1-a1)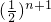 ]}若
]}若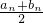 ≥0,则bn+1=
≥0,则bn+1=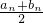 ,
,
bn+1-bn={a1+(b1-a1) }-{a1+(b1-a1)
}-{a1+(b1-a1) }=-(b1-a1)
}=-(b1-a1) <0,
<0,
所以bn+1<bn=,这与n是满足b1>b2>…>bn(n≥2)的最大整数矛盾.
因此n是满足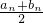 <0的最小整数.(12分)
<0的最小整数.(12分)
而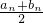 <0?
<0? <2n?log2
<2n?log2 <n,
<n,
因而n是满足log2 <n的最小整数.(14分)
<n的最小整数.(14分)
分析:(Ⅰ)分情况讨论,并分别做差ak-bk,从而可证明等比数列.
(Ⅱ)利用第一问的结论:数列{ak-bk}是等比数列,求出数列{n(bn-an)}的前n项和为Sn,再求极限得解.
(Ⅲ)如果n(n≥2)是满足b1>b2>…>bn的最大整数,利用已知条件,从而推出bn通项.再利用bn的性质推出因此n是满足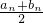 <0的最小整数.进而可推得n满足的条件(用a1,b1表示).
<0的最小整数.进而可推得n满足的条件(用a1,b1表示).
点评:本题是等比数列的综合题,考查等比数列证明,极限求法,不等式等有关知识,要求能力比较高,值得好好研究学习.
 ≥0时,bk-ak=
≥0时,bk-ak= -ak-1=
-ak-1= (bk-1ak-1),
(bk-1ak-1),当
 <0时,bk-ak=bk-1-
<0时,bk-ak=bk-1- =
= (bk-1ak-1),
(bk-1ak-1),所以不论哪种情况,都有bk-ak=
 (bk-1ak-1),又显然b1-a1>0,故数列{ak-bk}是等比数列(4分)
(bk-1ak-1),又显然b1-a1>0,故数列{ak-bk}是等比数列(4分)(Ⅱ)由(Ⅰ)知,bn-an=(b1-a1)=
 ,故n(bn-an)=(b1-a1)•
,故n(bn-an)=(b1-a1)•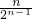 ,
,Sn=(b1-a1)(1+
 +
+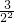 +…+
+…+ +
+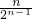 ),所以
),所以 Sn=(b1-a1)(1+
Sn=(b1-a1)(1+ +
+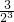 …+
…+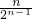 +
+ ),
),所以
 Sn=(b1-a1)(1+
Sn=(b1-a1)(1+ +
+ +…+
+…+ +
+ ),Sn=(b1-a1)[4(1-
),Sn=(b1-a1)[4(1- )-
)- ](7分)
](7分)又当a>1时

 =0,
=0, Sn=4(b1-a1).(8分)
Sn=4(b1-a1).(8分)(Ⅲ)当b1>b2>…>bn(n≥2)时,bk≠bk-1(2≤k≤n),由(2)知
 <0不成立,
<0不成立,故
 ≥0,从而对于2≤k≤n,有ak=ak-1,bk=
≥0,从而对于2≤k≤n,有ak=ak-1,bk= ,于是an=an-1=…=a1,
,于是an=an-1=…=a1,故bn=a1+(b1-a1)
 (10分)
(10分)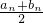 =
= {a1+[a1+(b1-a1)
{a1+[a1+(b1-a1)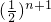 ]}若
]}若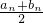 ≥0,则bn+1=
≥0,则bn+1=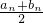 ,
,bn+1-bn={a1+(b1-a1)
 }-{a1+(b1-a1)
}-{a1+(b1-a1) }=-(b1-a1)
}=-(b1-a1) <0,
<0,所以bn+1<bn=,这与n是满足b1>b2>…>bn(n≥2)的最大整数矛盾.
因此n是满足
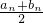 <0的最小整数.(12分)
<0的最小整数.(12分)而
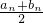 <0?
<0? <2n?log2
<2n?log2 <n,
<n,因而n是满足log2
 <n的最小整数.(14分)
<n的最小整数.(14分)分析:(Ⅰ)分情况讨论,并分别做差ak-bk,从而可证明等比数列.
(Ⅱ)利用第一问的结论:数列{ak-bk}是等比数列,求出数列{n(bn-an)}的前n项和为Sn,再求极限得解.
(Ⅲ)如果n(n≥2)是满足b1>b2>…>bn的最大整数,利用已知条件,从而推出bn通项.再利用bn的性质推出因此n是满足
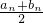 <0的最小整数.进而可推得n满足的条件(用a1,b1表示).
<0的最小整数.进而可推得n满足的条件(用a1,b1表示).点评:本题是等比数列的综合题,考查等比数列证明,极限求法,不等式等有关知识,要求能力比较高,值得好好研究学习.

练习册系列答案
相关题目