题目内容
【题目】已知函数f(x)满足f(x)=f( ![]() )且当x∈[
)且当x∈[ ![]() ,1]时,f(x)=lnx,若当x∈[
,1]时,f(x)=lnx,若当x∈[ ![]() ]时,函数g(x)=f(x)﹣ax与x轴有交点,则实数a的取值范围是( )
]时,函数g(x)=f(x)﹣ax与x轴有交点,则实数a的取值范围是( )
A.[﹣ ![]() ,0]
,0]
B.[﹣πlnπ,0]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,﹣
,﹣ ![]() ]
]
【答案】B
【解析】解:设x∈[1,π], 则 ![]() ∈[
∈[ ![]() ,1],
,1],
因为f(x)=f( ![]() )且当x∈[
)且当x∈[ ![]() ,1]时,
,1]时,
f(x)=lnx,
所以f(x)=f( ![]() )=ln
)=ln ![]() =﹣lnx,
=﹣lnx,
则f(x)= 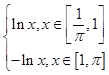 ,
,
在坐标系中画出函数f(x)的图象如图:
因为函数g(x)=f(x)﹣ax与x轴有交点,
所以直线y=ax与函数f(x)的图象有交点,
由图得,直线y=ax与y=f(x)的图象相交于点( ![]() ,﹣lnπ),
,﹣lnπ),
即有﹣lnπ= ![]() ,解得a=﹣πlnπ.
,解得a=﹣πlnπ.
由图象可得,实数a的取值范围是:[﹣πlnπ,0]
故选:B.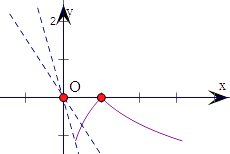

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目