题目内容
下列说法:
①“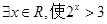 ”的否定是“
”的否定是“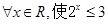 ”;
”;
②函数 的最小正周期是
的最小正周期是
③命题“函数 处有极值,则
处有极值,则 ”的否命题是真命题;
”的否命题是真命题;
④ 上的奇函数,
上的奇函数, 时的解析式是
时的解析式是 ,则
,则 时的解析式为
时的解析式为 其中正确的说法是 。
其中正确的说法是 。
①④
解析试题分析:因为存在性命题的否定是全称命题,所以①“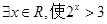 ”的否定是“
”的否定是“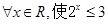 ”;正确。
”;正确。
因为 =
= ,所以②函数
,所以②函数 的最小正周期是
的最小正周期是 不正确。
不正确。
通过研究 在x=0时的导数值及极值情况知,③命题“函数
在x=0时的导数值及极值情况知,③命题“函数 处有极值,则
处有极值,则 ”的否命题是真命题;不正确。
”的否命题是真命题;不正确。
由奇偶函数确定分段函数的方法可得, 时的解析式为
时的解析式为 所以,④
所以,④ 上的奇函数,
上的奇函数, 时的解析式是
时的解析式是 ,则
,则 时的解析式为
时的解析式为 正确,综上知,正确的命题有①④。
正确,综上知,正确的命题有①④。
考点:本题主要考查全称命题与存在性命题的关系,三角函数图象和性质,函数的奇偶性。
点评:小综合题,这种类型的题目,在高考题中常常出现,扩大了知识考查的覆盖面,一般难度不大,主要运用数学的基础知识求解。

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 函数
函数 在
在 上单调递增;命题
上单调递增;命题 不等式
不等式 的解集是
的解集是 .若
.若 且
且 为真命题,则实数
为真命题,则实数 的取值范围是______.
的取值范围是______. 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设 于
于 于
于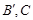 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ② ;
;  ; ④
; ④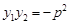 ; ⑤.
; ⑤. 
 ”的否定是 .
”的否定是 . B”,
B”, ,
, ”的否定是 .
”的否定是 .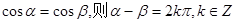 ;②函数
;②函数 的图象关于x=
的图象关于x= 对称;③函数
对称;③函数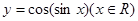 为偶函数,④函数
为偶函数,④函数 是周期函数,且周期为2
是周期函数,且周期为2 。
。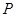 :
: ;则
;则 命题是;
命题是; ;
; (
(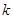 为正整数)的展开式中,
为正整数)的展开式中, 的系数小于90,则
的系数小于90,则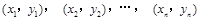 .若记
.若记 ,则回归直线
,则回归直线 必过点
必过点 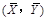 ;
;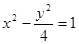 的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条;
的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条; ,给定条件
,给定条件 :
: ,条件
,条件 :
: ,若
,若 的取值范围为
的取值范围为