题目内容
在平面直角坐标系xOy中,圆C的方程为x2+y2=4,若直线kx-4y+16=0上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则K的取值范围 .
【答案】分析:由圆的方程找出圆心坐标与半径r,由题意得到直线kx-4y+16=0与圆C′:x2+y2=9有公共点,可得出圆心到直线的距离d小于等于3,利用点到直线的距离公式列出不等式,求出不等式的解集即可得到k的范围.
解答:解:由圆的方程x2+y2=4,得到圆心C(0,0),半径r=2,
∵直线kx-4y+16=0上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴直线kx-4y+16=0与圆C′:x2+y2=9有公共点,
∴圆心到直线的距离d≤3,即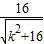 ≤3,
≤3,
解得:k≥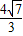 或k≤-
或k≤-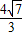 ,
,
则k的范围为(-∞,-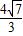 ]∪[
]∪[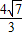 ,+∞).
,+∞).
故答案为:(-∞,-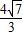 ]∪[
]∪[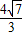 ,+∞).
,+∞).
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,圆的标准方程,以及不等式的解法,解题的关键是将条件化为“直线kx-4y+16=0与圆C′:x2+y2=9有公共点”.
解答:解:由圆的方程x2+y2=4,得到圆心C(0,0),半径r=2,
∵直线kx-4y+16=0上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴直线kx-4y+16=0与圆C′:x2+y2=9有公共点,
∴圆心到直线的距离d≤3,即
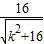 ≤3,
≤3,解得:k≥
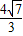 或k≤-
或k≤-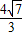 ,
,则k的范围为(-∞,-
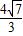 ]∪[
]∪[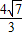 ,+∞).
,+∞).故答案为:(-∞,-
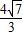 ]∪[
]∪[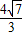 ,+∞).
,+∞).点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,圆的标准方程,以及不等式的解法,解题的关键是将条件化为“直线kx-4y+16=0与圆C′:x2+y2=9有公共点”.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是