题目内容
(本小题满分12分)棱柱![]() 中,
中,![]() 面
面![]() ,
,
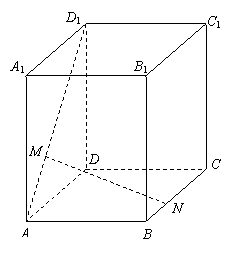 底面
底面![]() 为菱形,
为菱形,![]() ,
,![]() 分别在线段
分别在线段
![]() 上移动.
上移动.
(Ⅰ)若![]() 为线段
为线段![]() 中点, 是否存在
中点, 是否存在![]() ,
,
能使![]() 面
面![]() ,并说明理由
,并说明理由
(Ⅱ)若![]() 面
面![]() ,设
,设![]() ,
,
求动点![]() 的轨迹;
的轨迹;
(Ⅲ)设点![]() ,求点
,求点![]() ,
,![]() 距离最小值.
距离最小值.
(本小题满分12分)
解:过![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,则
,则![]() .
.![]() 是菱形,则
是菱形,则![]() ,因此
,因此![]() .
.
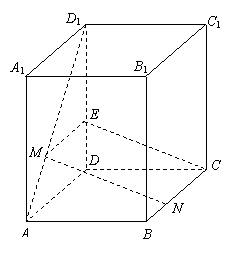 可得面
可得面![]() 面
面![]()
![]()
![]() 面
面![]() ,
,![]() .
.
则四边形![]() 为平行四边形 ,
为平行四边形 ,
因![]() ………………………………2分
………………………………2分
(Ⅰ)若![]() 为线段
为线段![]() 中点,
中点,
则![]()
![]() 为
为![]() 中点.…………………………………………3分
中点.…………………………………………3分
(Ⅱ)由已证四边形![]() 为平行四边形,
为平行四边形, ![]()
![]()
![]() …………………………5分
…………………………5分
平行四边形![]() 中
中![]()
![]() 即
即![]() ………………6分
………………6分
![]() 动点
动点![]() 的轨迹为双曲线
的轨迹为双曲线![]() 的一部分. ……………………7分
的一部分. ……………………7分
(Ⅲ)![]() ,
,
![]() …………………9分
…………………9分
令![]() 对称轴
对称轴![]()
当![]() 即
即![]() 时,
时, ![]() ,则
,则![]() ……………10分
……………10分
当![]() 即
即![]() 时,
时, ![]()
则![]() ……………………11分
……………………11分
当![]() 即
即![]() 时,
时, ![]() 无最小值. ………………………12分
无最小值. ………………………12分
【命题意图】本题考查线面关系的证明及二次函数求最值的问题,考查学生的空间想象能力和综合应用能力。

练习册系列答案
相关题目