题目内容
已知抛物线的焦点是F(0,-4),准线是y=4,则抛物线的方程是( )
分析:先确定抛物线的顶点在原点,焦点在y轴的负半轴,从而假设抛物线的标准方程,利用抛物线的焦点是F(0,-4),准线是y=4,即可求得抛物线的方程
解答:解:由题意,抛物线的顶点在原点,焦点在y轴的负半轴,设方程为x2=-2py(p>0)
∵抛物线的焦点是F(0,-4),准线是y=4
∴
=4
∴p=8
∴x2=-16y
∴y=-
x2
即抛物线的方程是y=-
x2
故选A.
∵抛物线的焦点是F(0,-4),准线是y=4
∴
| p |
| 2 |
∴p=8
∴x2=-16y
∴y=-
| 1 |
| 16 |
即抛物线的方程是y=-
| 1 |
| 16 |
故选A.
点评:本题以抛物线的性质为载体,考查抛物线的标准方程,确定抛物线的顶点在原点,焦点在y轴的负半轴是关键.

练习册系列答案
相关题目
 的焦点是F,定点A
的焦点是F,定点A ,
, 是抛物线上的动点,则
是抛物线上的动点,则 的最小值是_________。
的最小值是_________。 的焦点是F,点P是抛物线上的动点,又有点A(3,2),求
的焦点是F,点P是抛物线上的动点,又有点A(3,2),求 最小值,并求此时P点的坐标
最小值,并求此时P点的坐标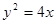 的焦点是F,点P是抛物线上的动点,又有点A(3,2),求
的焦点是F,点P是抛物线上的动点,又有点A(3,2),求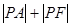 最小值,并求此时P点的坐标.
最小值,并求此时P点的坐标. 的焦点是F,点P是抛物线上的动点,又有点A(3,2),求
的焦点是F,点P是抛物线上的动点,又有点A(3,2),求 最小值,并求此时P点的坐标.
最小值,并求此时P点的坐标.