题目内容
抛物线顶点在坐标原点，以y轴为对称轴，过焦点且与y轴垂直的弦长为16，则抛物线方程为
x2=±16y
x2=±16y
．分析：过焦点且与y轴垂直的弦长叫做抛物线的通径，其长为2p，利用题意可得2p=16，从而得出p值，再结合抛物线的焦点所在的位置即可得出其方程．
解答：解：∵过焦点且与对称轴y轴垂直的弦长等于p的2倍．
∴所求抛物线方程为x2=±16y．
故答案为：x2=±16y．
∴所求抛物线方程为x2=±16y．
故答案为：x2=±16y．
点评：本题主要考查了抛物线的标准方程、抛物线的性质．属基础题．
练习册系列答案
高中必刷题系列答案
相关题目
轴上，其上一点
到焦点的距离为
，则抛物线的方程为（ ）
B．
C．
D．
，则抛物线方程是（ ）
B．
C．
D．
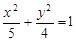的右焦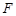点
重合，过点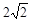
的直线与抛物线交于
，
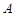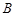两点.
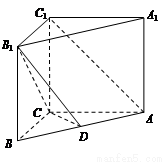
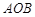的面积．