题目内容
已知数列{an}是各项均不为0的等差数列，公差为d，Sn为其前n项和，且满足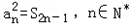
．数列{bn}满足
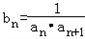，Tn为数列{bn}的前n项和．
（I）求a1，d和Tn；
（II）若对任意的n∈N*，不等式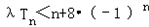
恒成立，求实数λ的取值范围．
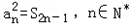．数列{bn}满足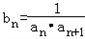，Tn为数列{bn}的前n项和．（I）求a1，d和Tn；
（II）若对任意的n∈N*，不等式
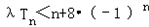恒成立，求实数λ的取值范围．解：（I）在
中，令n=1，n=2，
得
，即
，
解得a1=1，d=2，
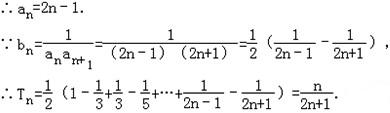
（II）（1）当n为偶数时，要使不等式
恒成立，
即需不等式
恒成立．
∵
，等号在n=2时取得．∴此时λ需满足λ＜25．
（2）当n为奇数时，要使不等式
恒成立，
即需不等式
恒成立．
∴
是随n的增大而增大，
∴
取得最小值﹣6．
∴此时λ需满足λ＜﹣21．
综合（1）（2）可得λ＜﹣21
∴?的取值范围是{λ|λ＜﹣21}．
中，令n=1，n=2，得
，即，解得a1=1，d=2，
（II）（1）当n为偶数时，要使不等式
恒成立，即需不等式
恒成立．∵
，等号在n=2时取得．∴此时λ需满足λ＜25．（2）当n为奇数时，要使不等式
恒成立，即需不等式
恒成立．∴
是随n的增大而增大，∴
取得最小值﹣6．∴此时λ需满足λ＜﹣21．
综合（1）（2）可得λ＜﹣21
∴?的取值范围是{λ|λ＜﹣21}．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
若一个数列各项取倒数后按原来的顺序构成等差数列，则称这个数列为调和数列．已知数列{an}是调和数列，对于各项都是正数的数列{xn}，满足
若一个数列各项取倒数后按原来的顺序构成等差数列，则称这个数列为调和数列．已知数列{an}是调和数列，对于各项都是正数的数列{xn}，满足
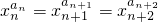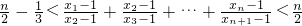（n∈N*）．
．
（n∈N*）．
．
（n∈N*）．
．