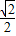题目内容
若不等式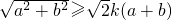 对任意正数a,b恒成立,则实数k的最大值为
对任意正数a,b恒成立,则实数k的最大值为
- A.

- B.1
- C.2
- D.

A
分析:由题意可得 ,由基本不等式可得
,由基本不等式可得  的最小值等于
的最小值等于 ,故k2≤
,故k2≤ ,从而得到实数k的最大值.
,从而得到实数k的最大值.
解答:由不等式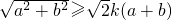 可得
可得  ,故k2 小于或等于
,故k2 小于或等于 的最小值.
的最小值.
∵ =
= ≥
≥ =
= ,故
,故 的最小值等于
的最小值等于 ,
,
故 k2≤ ,∴k≤
,∴k≤ ,
,
故选 A.
点评:本题考查不等式的性质,基本不等式的应用,求出 的最小值,是解题的关键.
的最小值,是解题的关键.
分析:由题意可得
 ,由基本不等式可得
,由基本不等式可得  的最小值等于
的最小值等于 ,故k2≤
,故k2≤ ,从而得到实数k的最大值.
,从而得到实数k的最大值.解答:由不等式
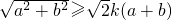 可得
可得  ,故k2 小于或等于
,故k2 小于或等于 的最小值.
的最小值.∵
 =
= ≥
≥ =
= ,故
,故 的最小值等于
的最小值等于 ,
,故 k2≤
 ,∴k≤
,∴k≤ ,
,故选 A.
点评:本题考查不等式的性质,基本不等式的应用,求出
 的最小值,是解题的关键.
的最小值,是解题的关键. 
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
若不等式
≥
k(a+b)对任意正数a,b恒成立,则实数k的最大值为( )
| a2+b2 |
| 2 |
A、
| ||||
| B、1 | ||||
| C、2 | ||||
D、
|
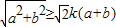 对任意正数a,b恒成立,则实数k的最大值为( )
对任意正数a,b恒成立,则实数k的最大值为( )