题目内容
(本小题14分)如图,在直三棱柱ABC—A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.
 (1)求证:平面B1AC⊥平面ABB1A1;
(1)求证:平面B1AC⊥平面ABB1A1;
(2)求C1到平面B1AC的距离;
(3)求三棱锥A1—AB1C的体积.
解:(1)证明:由直三棱柱性质,B1B⊥平面ABC,
∴B1B⊥AC,
又BA⊥AC,B1B∩BA=B,
∴AC⊥平面 ABB1A1,
又AC![]() 平面B1AC,
平面B1AC,
 ∴平面B1AC⊥平面ABB1A1.
∴平面B1AC⊥平面ABB1A1.
(2)解:∵A1C1∥AC, ![]() 平面B1AC
平面B1AC
∴A1C1∥平面B1AC
∴C1到平面B1AC的距离就是求A1到平面B1AC的距离
过A1做A1M⊥B1A1,垂足为M,连结CM,
∵平面B1AC⊥平面ABB1A,且平面B1AC∩平面ABB1A1=B1A,
∴A1M⊥平面B1AC.
![]()
∴C1到平面B1AC的距离为![]()
(3)解:∵直线B1C与平面ABC成30°角,
∴∠B1CB=30°.
可得B1C=2a,BC=![]() ,
,
∴![]()

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 km,用
km,用 的面积为14,
的面积为14, 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且


 ,
, 与
与 交于
交于 。设存在
。设存在 和
和 使
使 ,
, ,
, ,
, 。
。  ,
, 表示
表示
 的面积
的面积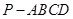 中,底面
中,底面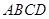 为矩形,侧棱
为矩形,侧棱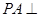 底面
底面 为
为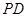 的中点.
的中点.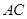 与
与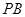 所成角的余弦值;
所成角的余弦值;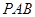 内找一点
内找一点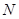 ,使
,使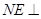 平面
平面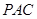 ,并分别求出点
,并分别求出点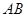 和
和 的距离.
的距离.
 中,
中, 平面
平面 ,
, ,
, ,
, 分别是
分别是 上
上 平面
平面 为
为 .
. 平面
平面 ;
; ,求直线
,求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值. 中,
中, ,点
,点 在边
在边 上,
上, 。
。 平面
平面 ;
; 是
是 的中点,求证:
的中点,求证: 平面
平面 .
.