题目内容
(本小题满分12分)
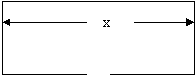
围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙(利用旧墙需维修)，其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙的长度为x(单位：m),修建此矩形场地围墙的总费用为y(单位：元).
(I)将y表示为x的函数；
(II)试确定x,使修建此矩形场地围墙的总费用最小，并求出最小总费用.
 |
(本小题满分12分)
.解：(I)如图，设矩形的另一边长为
m，
则
. …………3分
由已知
,得
, …………4分
所以y=225x+
w.w.w. .c. o.m ………………6分
(II)
…………8分
∴
.当且仅当225x=
时，等号成立. …………11分
即当x=24m时，修建围墙的总费用最小，最小总费用是10440元…………12分
练习册系列答案
阅读快车系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
