题目内容
数列![]() 首项
首项![]() ,前
,前![]() 项和
项和![]() 与
与![]() 之间满足
之间满足![]()
(1)求证:数列![]() 是等差数列 (2)求数列
是等差数列 (2)求数列![]() 的通项公式
的通项公式
(3)设存在正数![]() ,使
,使![]() 对于一切
对于一切![]() 都成立,求
都成立,求![]() 的最大值。
的最大值。
⑴证明略,⑵ ,⑶
,⑶![]() 的最大值是
的最大值是![]() .
.
解析:
(1)因为![]() 时,
时,![]() 得
得 ![]()
由题意 ![]()
![]()
又![]()
 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
(2)由(1)有![]()
![]()
![]() 时,
时,![]() .
.
又![]()

(3)设![]()
则
![]() 在
在![]() 上递增 故使
上递增 故使![]() 恒成立只需
恒成立只需![]()
又![]() 又
又![]()
![]() ,所以,
,所以,![]() 的最大值是
的最大值是![]() .
.

练习册系列答案
相关题目
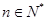 (
(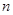 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前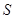 型数列。
型数列。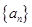 是首项
是首项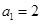 的
的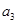 的值;
的值;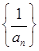 是
是 试求
试求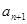 与
与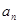 的递推关系,并证明
的递推关系,并证明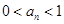 对
对