题目内容
已知正方体ABCD-A1B1C1D1的棱长为1,正方体内衣球O1与面ABCD,BCC1B1,ABB1A1均相切,正方体内另一球O2与面ADD1A1,A1B1C1D1,CDD1C1均相切,且两球外切,那么两球表面积之和的最小值是________.
(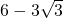 )π
)π
分析:设球O1、O2的半径分别为r1、r2,可得BD1=BO1+O1O2+O2D1=(1+ )(r1+r2)=
)(r1+r2)= ,从而得到r1+r2=
,从而得到r1+r2=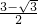 .再根据基本不等式,得r12+r22≥
.再根据基本不等式,得r12+r22≥ (r1+r2)2=
(r1+r2)2=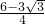 ,当且仅当r1=r2=
,当且仅当r1=r2=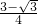 时等号成立,由此结合球的表面积公式,即可得到两球表面积之和的最小值.
时等号成立,由此结合球的表面积公式,即可得到两球表面积之和的最小值.
解答: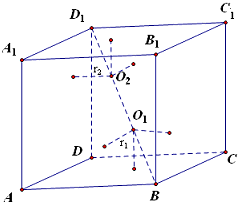 解:根据题意,得
解:根据题意,得
BD1=BO1+O1O2+O2D1= AA1=
AA1= ,
,
设球O1、O2的半径分别为r1、r2,根据正方体的性质和球与平面、球与球相切的性质,得BO1= r1,O1O2=r1+r2,O2D1=
r1,O1O2=r1+r2,O2D1= r2,
r2,
∴( +1)(r1+r2)=
+1)(r1+r2)= ,得r1+r2=
,得r1+r2=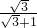 =
=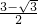
由基本不等式,得2(r12+r22)≥(r1+r2)2=3- ,
,
∴r12+r22≥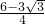 ,当且仅当r1=r2=
,当且仅当r1=r2=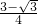 时等号成立
时等号成立
因此,两球表面积之和S1+S2=4π(r12+r22)≥(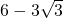 )π
)π
故答案为:(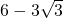 )π
)π
点评:本题给出正方体内两个相切的球分别与正方体的三个面相切,求两个球的表面积之和的最小值,着重考查了正方体的性质和球与平面、球与球相切的性质,基本不等式及球的表面积公式等知识,属于中档题.
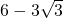 )π
)π分析:设球O1、O2的半径分别为r1、r2,可得BD1=BO1+O1O2+O2D1=(1+
 )(r1+r2)=
)(r1+r2)= ,从而得到r1+r2=
,从而得到r1+r2=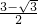 .再根据基本不等式,得r12+r22≥
.再根据基本不等式,得r12+r22≥ (r1+r2)2=
(r1+r2)2=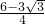 ,当且仅当r1=r2=
,当且仅当r1=r2=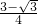 时等号成立,由此结合球的表面积公式,即可得到两球表面积之和的最小值.
时等号成立,由此结合球的表面积公式,即可得到两球表面积之和的最小值.解答:
 解:根据题意,得
解:根据题意,得BD1=BO1+O1O2+O2D1=
 AA1=
AA1= ,
,设球O1、O2的半径分别为r1、r2,根据正方体的性质和球与平面、球与球相切的性质,得BO1=
 r1,O1O2=r1+r2,O2D1=
r1,O1O2=r1+r2,O2D1= r2,
r2,∴(
 +1)(r1+r2)=
+1)(r1+r2)= ,得r1+r2=
,得r1+r2=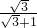 =
=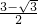
由基本不等式,得2(r12+r22)≥(r1+r2)2=3-
 ,
,∴r12+r22≥
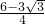 ,当且仅当r1=r2=
,当且仅当r1=r2=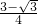 时等号成立
时等号成立因此,两球表面积之和S1+S2=4π(r12+r22)≥(
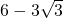 )π
)π故答案为:(
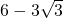 )π
)π点评:本题给出正方体内两个相切的球分别与正方体的三个面相切,求两个球的表面积之和的最小值,着重考查了正方体的性质和球与平面、球与球相切的性质,基本不等式及球的表面积公式等知识,属于中档题.

练习册系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.