题目内容
1.求满足下列条件的实数a的取值范围:(1)若关于x的不等式|x+2|+|x-3|<a解集非空;
(2)若关于x的不等式|x+2|+|x-3|≥a恒成立.
分析 (1)容易求出|x+2|+|x-3|的最小值为5,而根据不等式|x+2|+|x-3|<a的解集非空便知该不等式有解,从而有5<a,这样即求出实数a的取值范围;
(2)根据上面知|x+2|+|x-3|的最小值为5,而不等式|x+2|+|x-3|≥a恒成立,从而有5≥a,这即得出了实数a的取值范围.
解答 解:(1)根据条件知不等式|x+2|+|x-3|<a有解;
|x+2|+|x-3|≥|(x+2)-(x-3)|=5;
即|x+2|+|x-3|的最小值为5;
∴5<a;
即a>5;
∴实数a的取值范围为(5,+∞);
(2)|x+2|+|x-3|的最小值为5,且不等式|x+2|+|x-3|≥a恒成立;
∴5≥a;
即a≤5;
∴实数a的取值范围为(-∞,5].
点评 考查绝对值不等式公式:|a|+|b|≥|a-b|,清楚当不等式有解和不等式恒成立时求参数的取值范围的方法的不同.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若变量x,y满足约束条件$\left\{\begin{array}{l}2x-y≤0\\ x-3y+5≥0\\ y≥1\end{array}\right.$,则${(\frac{1}{2})^{x+y-2}}$的最大值是( )
| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
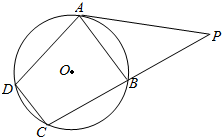 如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.
如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.