题目内容
已知函数 ,
,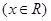 .
.
(1)求证:不论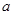 为何实数
为何实数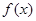 在
在 上为增函数;
上为增函数;
(2)若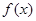 为奇函数,求
为奇函数,求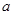 的值;
的值;
(3)在(2)的条件下,求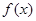 在区间
在区间 上的最小值.
上的最小值.
 ,
,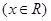 .
.(1)求证:不论
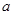 为何实数
为何实数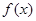 在
在 上为增函数;
上为增函数;(2)若
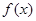 为奇函数,求
为奇函数,求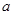 的值;
的值;(3)在(2)的条件下,求
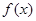 在区间
在区间 上的最小值.
上的最小值.(1)详见解析
(2)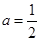
(3)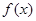 在区间
在区间 上的最小值为
上的最小值为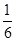 .
.
(2)
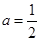
(3)
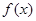 在区间
在区间 上的最小值为
上的最小值为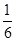 .
.(1)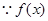 的定义域为R, 任取
的定义域为R, 任取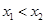 ,
,
则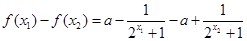 =
=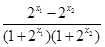 .
.
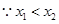 ,∴
,∴ 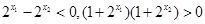 .
.
∴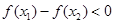 ,即
,即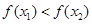 .
.
所以不论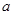 为何实数
为何实数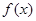 总为增函数.
总为增函数.
(2)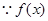 在
在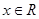 上为奇函数,
上为奇函数,
∴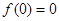 ,即
,即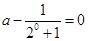 .
.
解得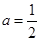 .
.
(3)由(2)知,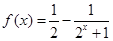 ,
,
由(1)知,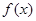 为增函数,
为增函数,
∴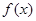 在区间
在区间 上的最小值为
上的最小值为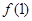 .
.
∵ ,
,
∴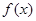 在区间
在区间 上的最小值为
上的最小值为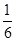 .
.
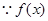 的定义域为R, 任取
的定义域为R, 任取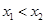 ,
,则
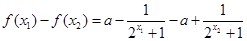 =
=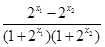 .
. 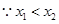 ,∴
,∴ 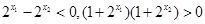 .
.∴
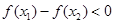 ,即
,即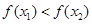 .
.所以不论
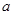 为何实数
为何实数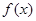 总为增函数.
总为增函数. (2)
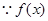 在
在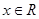 上为奇函数,
上为奇函数,∴
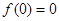 ,即
,即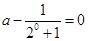 .
. 解得
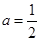 .
.(3)由(2)知,
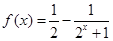 ,
, 由(1)知,
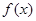 为增函数,
为增函数,∴
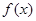 在区间
在区间 上的最小值为
上的最小值为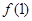 .
.∵
 ,
,∴
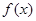 在区间
在区间 上的最小值为
上的最小值为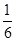 .
.
练习册系列答案
相关题目
 .
.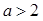 ,求
,求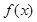 在
在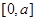 上的最大值.
上的最大值.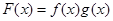 是R上的奇函数,当
是R上的奇函数,当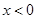 时,
时,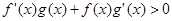 ,且
,且 ,则不等式
,则不等式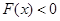 的解集是( )
的解集是( )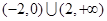
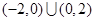
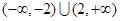
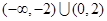
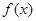 是定义在
是定义在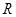 上的奇函数,且
上的奇函数,且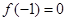 ,若不等式
,若不等式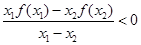 对区间
对区间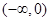 内任意的两个不相等的实数
内任意的两个不相等的实数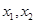 都成立,则不等式
都成立,则不等式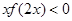 的解集是 。
的解集是 。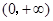 上单调递增的是( )
上单调递增的是( )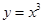
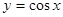
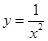
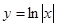
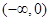 上单调递增的是( )
上单调递增的是( )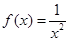
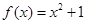
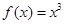
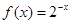
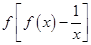 =2,则
=2,则 的值是( )
的值是( )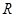 上的奇函数
上的奇函数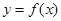 在
在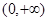 上单调递增,且
上单调递增,且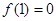 ,则不等式
,则不等式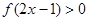 的解集为 .
的解集为 .