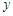题目内容
某工厂三个车间共有工人1000名,各车间男、女工人数如表:
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知y≥185,z≥185,求第三车间中女工比男工少的概率.
分析:(1)在抽样过程中每个个体被抽到的概率是一样的,抽到第二车间男工的概率是0.15,用x除以1000就得到0.15,算出x的值.
(2)先做出第三车间的总人数,根据每个个体被抽到的概率,做出总人数.
(3)由y+z=400,且y≥185,z≥185,得到满足条件的(y,z),列举出所有的情况,即总是件数,再看女工比男工少有几组,根据古典概型公式得到结果.
(2)先做出第三车间的总人数,根据每个个体被抽到的概率,做出总人数.
(3)由y+z=400,且y≥185,z≥185,得到满足条件的(y,z),列举出所有的情况,即总是件数,再看女工比男工少有几组,根据古典概型公式得到结果.
解答:解:(1)由题意可知
=0.15,x=150;
(2)由题意可知第三车间共有工人数为1000-(173+177)-(100+150)=400名,
则设应在第三车间级抽取m名工人,则
=
,m=20.
(3)由题意可知y+z=400,且y≥185,z≥185,满足条件的(y,z)
有(185,215),(186,214)…(215,185)第一个数字是连续的整数,有215-185+1=31个整数因此共有31组.
设事件A:第三车间中女工比男工少,即y<z,满足条件的(y,z)
有(185,215),(186,214)…(199,201),共有199-185+1=15组.
故P(A)=
.
| x |
| 1000 |
(2)由题意可知第三车间共有工人数为1000-(173+177)-(100+150)=400名,
则设应在第三车间级抽取m名工人,则
| 50 |
| 1000 |
| m |
| 400 |
(3)由题意可知y+z=400,且y≥185,z≥185,满足条件的(y,z)
有(185,215),(186,214)…(215,185)第一个数字是连续的整数,有215-185+1=31个整数因此共有31组.
设事件A:第三车间中女工比男工少,即y<z,满足条件的(y,z)
有(185,215),(186,214)…(199,201),共有199-185+1=15组.
故P(A)=
| 15 |
| 31 |
点评:本题考查抽样和古典概型的概率,高考时这个知识点常以选择和填空形式出现,通过对现实生活中实际问题进行简单随机抽样,感知应用数学知识解决实际问题的方法.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
(本小题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
| 第一车间 | 第二车间 | 第三车间 | |
| 女工 | 173 | 100 |
|
| 男工 | 177 |
|
|
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知![]() ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.
(本小题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
|
|
第一车间 |
第二车间 |
第三车间 |
|
女工 |
173 |
100 |
|
|
男工 |
177 |
|
|
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知 ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.
(本小题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
|
|
第一车间 |
第二车间 |
第三车间 |
|
女工 |
173 |
100 |
|
|
男工 |
177 |
|
|
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知 ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.