Question

选修4-1：几何证明选讲：
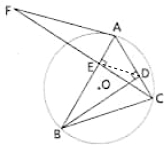
如图，已知⊙为△ABC的外接圆，AF切⊙O于点A，交△ABC的高CE的延长线于点F，BD⊥AC．证明：
（1）∠F=∠DBC；
（2）．

Answer 1

证明：（1）连接ED，则

∵AF切⊙O于点A，∴∠FAE=∠DCN
∵BD⊥AC，FE⊥AB
∴∠AEF=∠BDC=90″
∴∠F=∠DBC；
（2）∵BD⊥AC，CE⊥AB
∴D，E，B，C四点共圆
∴∠DEC=∠DBC
∵∠F=∠DBC
∴∠DEC=∠F
∴DE∥AF
∴
分析：（1）连接ED，利用AF切⊙O于点A，可得∠FAE=∠DCN，再证明∠AEF=∠BDC=90″，即可证得∠F=∠DBC；
（2）由BD⊥AC，CE⊥AB，可得D，E，B，C四点共圆，从而有∠DEC=∠DBC，利用∠F=∠DBC，可得∠DEC=∠F，从而DE∥AF，故可证得结论．
点评：本题考查圆中的比例线段，考查四点共圆，考查学生分析问题的能力，属于中档题．