题目内容
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
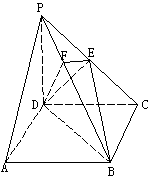
(1)证明PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小。
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小。
| 解:(1)证明:连结AC,AC交BD于O,连结EO。 ∵底面ABCD是正方形, ∴点O是AC的中点 在 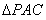 中,EO是中位线, 中,EO是中位线,∴PA // EO 而 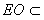 平面EDB且 平面EDB且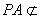 平面EDB, 平面EDB, 所以,PA // 平面EDB 。 |
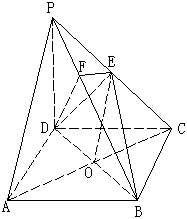 |
(2)∵PD⊥底面ABCD且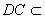 底面ABCD, 底面ABCD,∴ 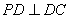 ∵PD=DC,可知 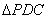 是等腰直角三角形,而DE是斜边PC的中线, 是等腰直角三角形,而DE是斜边PC的中线, ∴ 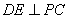 。 ① 。 ① 同样由PD⊥底面ABCD,得PD⊥BC。 ∵底面ABCD是正方形,有DC⊥BC, ∴BC⊥平面PDC。 而 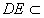 平面PDC, 平面PDC,∴ 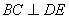 。 ② 。 ②由①和②推得 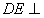 平面PBC。 平面PBC。而 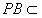 平面PBC, 平面PBC,∴ 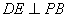 又 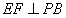 且 且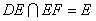 , ,所以PB⊥平面EFD。 (3)由(2)知, 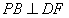 ,故∠EFD是二面角C-PB-D的平面角。 ,故∠EFD是二面角C-PB-D的平面角。由(2)知, 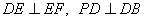 。 。设正方形ABCD的边长为a,则 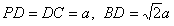 , ,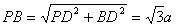 , ,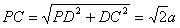 , ,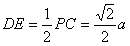 。 。在 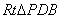 中, 中,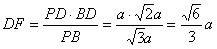 。 。在 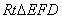 中,sin∠EFD= 中,sin∠EFD=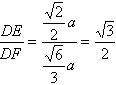 , ,∴∠EFD= 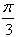 。 。所以,二面角C-PB-D的大小为 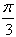 。 。 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.