题目内容
已知| a |
| b |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
(2)若直线l:y=3x+m(m≠0)与曲线C交于A,B两点,D(0,-1)且|
| AD |
| BD |
分析:(1)由已知x2=3+3y2,由此能得到P的轨迹方程.
(2)设A(x1,y1),B(x2,y2),AB中点E坐标为(x0,y0).
,消去y得:26x2+18mx+3m2+3=0
由韦达定理和根的判别式能够求出m的值.
(2)设A(x1,y1),B(x2,y2),AB中点E坐标为(x0,y0).
|
由韦达定理和根的判别式能够求出m的值.
解答:解:(1)由已知
2=3
2(2分)
即x2=3+3y2,所以P的轨迹方程为
-y2=1(5分)
(2)设A(x1,y1),B(x2,y2),AB中点E坐标为(x0,y0).
,消去y得:26x2+18mx+3m2+3=0
由韦达定理得:x1+x2=-
,则x0=-
,y0=-
,(8分)
则AB垂直平分线方程为y+
=-
(x+
),
又点D(-1,0)在AB的垂直平分线上,代入方程得m=
(11分)
(注:也可由DE的斜率为-
,得
=-
,解得m=
)
由△>0,得m2>26
所以m=
时,直线l:y=3x+m,m≠0与双曲线C相交,符合题意,
所以m=
.(12分)
| a |
| b |
即x2=3+3y2,所以P的轨迹方程为
| x2 |
| 3 |
(2)设A(x1,y1),B(x2,y2),AB中点E坐标为(x0,y0).
|
由韦达定理得:x1+x2=-
| 9m |
| 13 |
| 9m |
| 26 |
| m |
| 26 |
则AB垂直平分线方程为y+
| m |
| 26 |
| 1 |
| 3 |
| 9m |
| 26 |
又点D(-1,0)在AB的垂直平分线上,代入方程得m=
| 13 |
| 2 |
(注:也可由DE的斜率为-
| 1 |
| 3 |
-
| ||
-
|
| 1 |
| 3 |
| 13 |
| 2 |
由△>0,得m2>26
所以m=
| 13 |
| 2 |
所以m=
| 13 |
| 2 |
点评:本题考查直线和圆锥曲线的位置关系的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
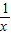 ,g(x)=x,已知A(x,0),(x>0),如图,过A作平行于y轴的直线交y=g(x)的图象于A1,交y=f(x)的图象于P1,要过P1作平行于x轴的直线交y=g(x)于A2,再过A2作平行于y轴的直线交y=f(x)于P2,…,这样一直作下去;设△A1P1A2的面积为S1,…,△AkPkAk+1的面积为Sk,数列{Sn}的前n项和为Tn,并设Pn(xn,yn).
,g(x)=x,已知A(x,0),(x>0),如图,过A作平行于y轴的直线交y=g(x)的图象于A1,交y=f(x)的图象于P1,要过P1作平行于x轴的直线交y=g(x)于A2,再过A2作平行于y轴的直线交y=f(x)于P2,…,这样一直作下去;设△A1P1A2的面积为S1,…,△AkPkAk+1的面积为Sk,数列{Sn}的前n项和为Tn,并设Pn(xn,yn).