题目内容
设f(x)=ln(x+1)+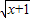 +ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y=
+ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y= x在(0,0)点相切.
x在(0,0)点相切.(I)求a,b的值;
(II)证明:当0<x<2时,f(x)<
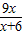 .
.
【答案】分析:(I)由y=f(x)过(0,0),可求b的值,根据曲线y=f(x)与直线 在(0,0)点相切,利用导函数,可求a的值;
在(0,0)点相切,利用导函数,可求a的值;
(II)由(I)知f(x)=ln(x+1)+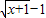 ,由均值不等式,可得
,由均值不等式,可得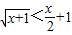 ,构造函数k(x)=ln(x+1)-x,可得ln(x+1)<x,从而当x>0时,f(x)<
,构造函数k(x)=ln(x+1)-x,可得ln(x+1)<x,从而当x>0时,f(x)<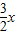 ,记h(x)=(x+6)f(x)-9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证.
,记h(x)=(x+6)f(x)-9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证.
解答:(I)解:由y=f(x)过(0,0),∴f(0)=0,∴b=-1
∵曲线y=f(x)与直线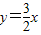 在(0,0)点相切.
在(0,0)点相切.
∴y′|x=0=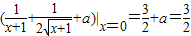
∴a=0;
(II)证明:由(I)知f(x)=ln(x+1)+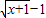
由均值不等式,当x>0时,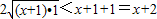 ,∴
,∴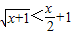 ①
①
令k(x)=ln(x+1)-x,则k(0)=0,k′(x)=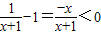 ,∴k(x)<0
,∴k(x)<0
∴ln(x+1)<x,②
由①②得,当x>0时,f(x)<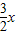
记h(x)=(x+6)f(x)-9x,则当0<x<2时,h′(x)=f(x)+(x+6)f′(x)-9
<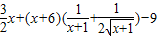 <
<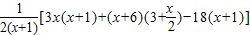
=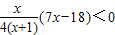
∴h(x)在(0,2)内单调递减,又h(0)=0,∴h(x)<0
∴当0<x<2时,f(x)<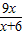 .
.
点评:本题考查导数知识的运用,考查导数的几何意义,考查构造法的运用,考查不等式的证明,正确构造函数是解题的关键.
 在(0,0)点相切,利用导函数,可求a的值;
在(0,0)点相切,利用导函数,可求a的值;(II)由(I)知f(x)=ln(x+1)+
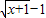 ,由均值不等式,可得
,由均值不等式,可得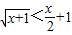 ,构造函数k(x)=ln(x+1)-x,可得ln(x+1)<x,从而当x>0时,f(x)<
,构造函数k(x)=ln(x+1)-x,可得ln(x+1)<x,从而当x>0时,f(x)<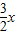 ,记h(x)=(x+6)f(x)-9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证.
,记h(x)=(x+6)f(x)-9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证.解答:(I)解:由y=f(x)过(0,0),∴f(0)=0,∴b=-1
∵曲线y=f(x)与直线
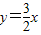 在(0,0)点相切.
在(0,0)点相切.∴y′|x=0=
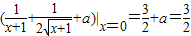
∴a=0;
(II)证明:由(I)知f(x)=ln(x+1)+
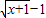
由均值不等式,当x>0时,
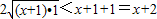 ,∴
,∴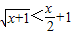 ①
①令k(x)=ln(x+1)-x,则k(0)=0,k′(x)=
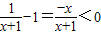 ,∴k(x)<0
,∴k(x)<0∴ln(x+1)<x,②
由①②得,当x>0时,f(x)<
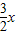
记h(x)=(x+6)f(x)-9x,则当0<x<2时,h′(x)=f(x)+(x+6)f′(x)-9
<
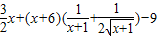 <
<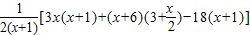
=
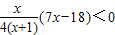
∴h(x)在(0,2)内单调递减,又h(0)=0,∴h(x)<0
∴当0<x<2时,f(x)<
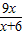 .
.点评:本题考查导数知识的运用,考查导数的几何意义,考查构造法的运用,考查不等式的证明,正确构造函数是解题的关键.

练习册系列答案
相关题目