Question

设y=f（x）是定义在R上的偶函数，满足f（x+1）=-f（x），且在[-1，0]上是增函数，给出下列关于函数y=f（x）的判断：
①y=f（x）是周期函数；
②y=f（x）的图象关于直线x=1对称；
③y=f（x）在[0，1]上是增函数；
④f(

1

2

)=0．
其中正确判断的序号是

 

．（把你认为正确判断的序号都填上）

Answer 1

分析：由题意y=f（x）是定义在R上的偶函数，满足f（x+1）=-f（x），可以知道该函数的周期为2，在利用f（x）为偶函数且在[-1，0]上为增函数，可以由题意画出一个草图即可判断．

解答：解：因为f（x+1）=-f（x）  所以f（x+2）=-f（x+1）=f（x），由函数的周期定义可知该函数的周期为2，由于f（x）为定义在R上的偶函数且在[-1，0]上为单调递增函数，所以由题意可以画出一下的函数草图为：

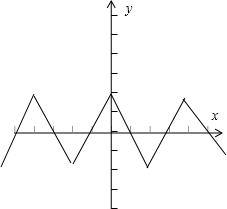
由图及题中条件可以得到：
①正确，周期T=2；
②由图可以知道该函数关于x=1对称，所以②正确；
③有已知条件 y=f（x）是定义在R上的偶函数且在[-1，0]上是增函数，所以y=f（x）在[0，1]上为单调递减函数，故③错；
④对于f（x+1）=-f（x），令x=-

1

2

，得到：f（

1

2

）=-f（-

1

2

）?f(

1

2

)=-f(

1

2

)（因为函数f（x）为偶函数）∴f(

1

2

)=0故④正确．

点评：此题考查了函数的周期性，对称性及有抽象函数式子赋值的方法，还考查了学生对于抽象问题的具体化及数形结合的思想．