题目内容
在△ABC中，cosA=
，cosB=
，则△ABC的形状是（ ）
| ||
| 5 |
3
| ||
| 10 |
| A．锐角三角形 | B．钝角三角形 | C．直角三角形 | D．等边三角形 |
由A和B都为三角形的内角，cosA=
，cosB=
，
得到：sinA=
，sinB=
，
则cosC=cos[180°-（A+B）]=-cos（A+B）=-cosAcosB+sinAsinB=-
×
+
×
=-
＜0，
∴C∈（90°，180°），即角C为钝角，
则△ABC的形状是钝角三角形．
故选B．
| ||
| 5 |
3
| ||
| 10 |
得到：sinA=
2
| ||
| 5 |
| ||
| 10 |
则cosC=cos[180°-（A+B）]=-cos（A+B）=-cosAcosB+sinAsinB=-
| ||
| 5 |
3
| ||
| 10 |
2
| ||
| 5 |
| ||
| 10 |
| ||
| 10 |
∴C∈（90°，180°），即角C为钝角，
则△ABC的形状是钝角三角形．
故选B．
练习册系列答案
相关题目
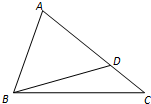如图，在△ABC中，cos∠ABC=