题目内容
(2012•济南三模)已知函数f(x)=
asinx+bcos(x-
)的图象经过点(
,
),(
,0).
(1)求实数a,b的值;
(2)求函数f(x)的周期及单调增区间.
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 7π |
| 6 |
(1)求实数a,b的值;
(2)求函数f(x)的周期及单调增区间.
分析:(1)由函数的图象经过点(
,
),(
,0),建立方程,即可求得实数a,b的值;
(2)先将函数化简为f(x)=sin(2x-
),由此可求函数f(x)的周期及单调增区间.
| π |
| 3 |
| 1 |
| 2 |
| 7π |
| 6 |
(2)先将函数化简为f(x)=sin(2x-
| π |
| 6 |
解答:解:(1)∵函数f(x)=
asinx+bcos(x-
)的图象经过点(
,
),(
,0).
∴
------(3分)
∴a=1,b=-1------(6分)
(2)由(1)知:函数f(x)=
asinx+bcos(x-
)=
sinx-cos(x-
)=sin(x-
)
∴函数f(x)的周期T=2π (10分)
由2kπ-
≤x-
≤2kπ+
,解得2kπ-
≤x≤2kπ+
,k∈Z.
即函数的增区间[2kπ-
,2kπ+
]k∈Z.(12分)
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 7π |
| 6 |
∴
|
∴a=1,b=-1------(6分)
(2)由(1)知:函数f(x)=
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 6 |
∴函数f(x)的周期T=2π (10分)
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
即函数的增区间[2kπ-
| π |
| 3 |
| 2π |
| 3 |
点评:本题考查三角函数的化简,考查三角函数的性质,考查学生的计算能力,正确化简函数是关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
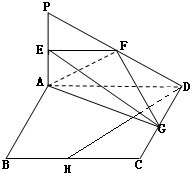 (2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.