题目内容
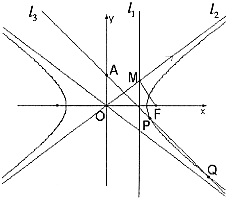 如图,已知双曲线C:
如图,已知双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
(I)求证:
| OM |
| MF |
(II)若|
| MF |
| ||
| 2 |
(III)在(II)的条件下,直线l3过点A(0,1)与双曲线C右支交于不同的两点P、Q且P在A、Q之间,满足
| AP |
| AQ |
分析:(Ⅰ)可求得点M(
,
),F(c,0),
=(
,-
),计算
•
=0即可;
(Ⅱ)由e=
,可得a2=2b2,又|
|=1,可求得双曲线C的方程为:
-y2=1;
(Ⅲ)设l3:y=kx+1,点P(x1,y1),Q(x2,y2),由
联立得(1-2k2)x2-4kx+4=0,结合l3与双曲线C右支交于不同的两点P、Q,列关系式可求得-1<k<-
,再结合
=λ
,即可求得λ的取值范围.
| a2 |
| c |
| ab |
| c |
| MF |
| b2 |
| c |
| ab |
| c |
| OM |
| MF |
(Ⅱ)由e=
| ||
| 2 |
| MF |
| x2 |
| 2 |
(Ⅲ)设l3:y=kx+1,点P(x1,y1),Q(x2,y2),由
|
| ||
| 2 |
| AP |
| AQ |
解答:证明:(I)∵右准线l1:x=
,渐近线l2:y=
x,
∴M(
,
),
∵F(c,0),c2=a2+b2,
∴
=(
,
),
=(c-
,-
)=(
,-
),
∵
•
=
-
=0,
∴
⊥
…(3分)
(II)∵e=
,
∴
=
=
,
∴a2=2b2,
∵|
|=1,
∴
+
=1,
∴
=1
∴双曲线C的方程为:
-y2=1…(7分)
(III)由题意可得0<λ<1…(8分)
证明:设l3:y=kx+1,点P(x1,y1),Q(x2,y2)
由
得(1-2k2)x2-4kx+4=0∵l3与双曲线C右支交于不同的两点P、Q
∴
∴
,
∴-1<k<-
…(11分)
∵
=λ
,
∴(x1,y1-1)=λ(x2,y2-1),得x1=λx2
∵-1<k<-
,
∴0<2k2-1<1,
∴
>4,
∴(1+λ)2>4λ,
∴λ2-2λ+1>0
∴λ的取值范围是(0,1)…(13分)
| a2 |
| c |
| b |
| a |
∴M(
| a2 |
| c |
| ab |
| c |
∵F(c,0),c2=a2+b2,
∴
| OM |
| a2 |
| c |
| ab |
| c |
| MF |
| a2 |
| c |
| ab |
| c |
| b2 |
| c |
| ab |
| c |
∵
| OM |
| MF |
| a2b2 |
| c2 |
| a2b2 |
| c2 |
∴
| OM |
| MF |
(II)∵e=
| ||
| 2 |
∴
| b |
| a |
| e2-1 |
| ||
| 2 |
∴a2=2b2,
∵|
| MF |
∴
| b4 |
| c2 |
| a2b2 |
| c2 |
∴
| b2(b2+a2) |
| c2 |
∴双曲线C的方程为:
| x2 |
| 2 |
(III)由题意可得0<λ<1…(8分)
证明:设l3:y=kx+1,点P(x1,y1),Q(x2,y2)
由
|
∴
|
|
∴-1<k<-
| ||
| 2 |
∵
| AP |
| AQ |
∴(x1,y1-1)=λ(x2,y2-1),得x1=λx2
|
∵-1<k<-
| ||
| 2 |
∴0<2k2-1<1,
∴
| (1+λ)2 |
| λ |
∴(1+λ)2>4λ,
∴λ2-2λ+1>0
∴λ的取值范围是(0,1)…(13分)
点评:本题考查直线与圆锥曲线的综合问题,着重考查双曲线的标准方程与简单几何性质及其应用,难点在于(Ⅲ)λ的范围的求解,方程思想与转化思想的综合运用,属于较难的题.

练习册系列答案
相关题目
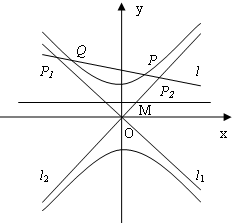 如图,已知双曲线C:
如图,已知双曲线C: 如图,已知双曲线C:
如图,已知双曲线C: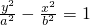 (a>0,b>0)的离心率e=
(a>0,b>0)的离心率e= ,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且
,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且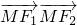 =-1.
=-1.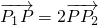 ,求|
,求| |的最小值.
|的最小值. (a>0,b>0)的离心率e=
(a>0,b>0)的离心率e= ,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且
,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且 =-1.
=-1.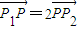 ,求|
,求| |的最小值.
|的最小值.
 (a>0,b>0)的离心率e=
(a>0,b>0)的离心率e=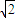 ,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且
,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且 =-1.
=-1.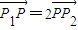 ,求|
,求| |的最小值.
|的最小值.