题目内容
已知椭圆C的中心在原点,焦点在x轴上,左右焦点分别为F1,F2;且![]() 点
点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A![]() 、B两点,且△AF2B的面积为
、B两点,且△AF2B的面积为![]() ,求以F2为圆
,求以F2为圆
心且与直线l相切的圆的方程.
解:(1)设椭圆的方程为![]() ,由题意可得:
,由题意可得:
![]() 椭圆C两焦点坐标分别为F1(-1,0),F2(1,0). ………………2分
椭圆C两焦点坐标分别为F1(-1,0),F2(1,0). ………………2分
![]()
![]() ,又c=1, b2=4-l=3,
,又c=1, b2=4-l=3,
故椭圆的方程为![]() .…………4分
.…………4分
(2)当直线l⊥x轴,计算得到:![]()
![]() ,不符合题意,…………………6分
,不符合题意,…………………6分
当直线l与x轴不垂直时,设直线l的方程为:y=k(x+1),
由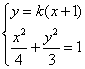 ,消去y得
,消去y得![]()
显然△>O成立,设![]()
则![]() ………………8分
………………8分
又![]()
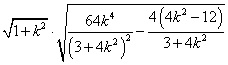
即![]() ' …………………………………………10分
' …………………………………………10分
又圆F2的半径![]() ……………………………11分
……………………………11分
所以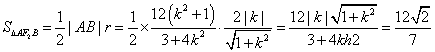
化简,得![]() ,即
,即![]() ,解得k=±1,……l3分
,解得k=±1,……l3分
所以,![]() ,故圆F2的方程为:(x-1)2+y2=2.……………l4分
,故圆F2的方程为:(x-1)2+y2=2.……………l4分
(2)另解:设直线l的方程为x=ty-1,[来源:学科网]
由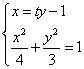 ,消去x得
,消去x得![]() ,△>O恒成立,
,△>O恒成立,
设![]() ,则
,则![]()
所以![]()

又圆F2的半径为![]()
所以![]()
![]() ,解得t2=1,
,解得t2=1,
所以![]() .故圆F2的方程为:
.故圆F2的方程为:![]()

练习册系列答案
相关题目

 。
。