题目内容

在二面角α-l-β中，A∈l，B∈l，AC?α，BD?β，且AC⊥l，BD⊥l，已知AB=1，AC=BD=1，CD=
5
，则二面角α-l-β的余弦值为
-1
-1
．
分析：如图所示．由于
CD
=
CA
+
AB
+
BD
，利用数量积的性质可得
CD
2=(
CA
+
AB
+
BD
)2=
CA
2+
AB
2+
BD
2+2
CA
•
AB
+2
CA
•
BD
+2
AB
•
BD
，又CA⊥AB，AB⊥BD，可得
CA
•
AB
=
AB
•
BD
=0．进而得出．
解答：解：如图所示．
∵
CD
=
CA
+
AB
+
BD
，
∴
CD
2=(
CA
+
AB
+
BD
)2=
CA
2+
AB
2+
BD
2+2
CA
•
AB
+2
CA
•
BD
+2
AB
•
BD
，
∵CA⊥AB，AB⊥BD，∴
CA
•
AB
=
AB
•
BD
=0．
∴(
5
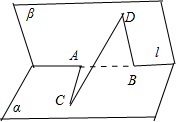
)2=12+12+12+0+2×1×1×cos＜
CA
，
BD
＞+0，
化为cos＜
CA
，
BD
＞=1，
∴二面角α-l-β的平面角为平角，其余弦值为-1．
故答案为-1．
点评：本题考查了利用向量的夹角求二面角的平面角的方法，属于中档题．
练习册系列答案
相关题目
4、在二面角α-l-β中，平面α的法向量为n，平面β的法向量为m，若＜n，m＞=130°，则二面角α-l-β的大小为（　　）
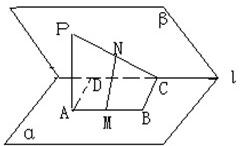精英家教网如图：在二面角α-l-β中，A、B∈α，C、D∈l，ABCD为矩形，p∈β，PA⊥α，且PA=AD，M、N依次是AB、PC的中点，
（1）求二面角α-l-β的大小
（2）求证：MN⊥AB
（3）求异面直线PA和MN所成角的大小．
在二面角α-l-β中，A∈l，AC?α，BD?β，且AC⊥l，BD⊥l，已知AB=1，AC=BD=2，CD=
5
，则二面角α-l-β的余弦值为
1
2
或-
1
2
1
2
或-
1
2
．
在二面角α-l-β中，A∈l，B∈l，AC?α，BD?β，且AC⊥l，BD⊥l，已知AB=1，AC=BD=2，CD=
5
，则二面角α-l-β的余弦值为
1
2
1
2
．
在二面角α-l-β中，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，若AB=AC=2，BD=CD=1，则二面角α-l-β的大小等于（　　）[

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网