题目内容
已知 在区间
在区间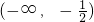 上是增函数,则实数a的取值范围是________.
上是增函数,则实数a的取值范围是________.
-1≤a<
分析:用复合函数的单调性来求解,令g(x)=x2-ax-a.由“f(x)=log g(x)在(-∞,-
g(x)在(-∞,- )上为增函数”,可知g(x)应在(-∞,-
)上为增函数”,可知g(x)应在(-∞,- )上为减函数且g(x)>0在(-∞,-
)上为减函数且g(x)>0在(-∞,- )上恒成立.再用“对称轴在区间的右侧,且最小值大于零”求解可得结果.
)上恒成立.再用“对称轴在区间的右侧,且最小值大于零”求解可得结果.
解答:令g(x)=x2-ax-a.
∵f(x)=log g(x)在(-∞,-
g(x)在(-∞,- )上为增函数,
)上为增函数,
∴g(x)应在(-∞,- )上为减函数且g(x)>0
)上为减函数且g(x)>0
在(-∞,- )上恒成立.
)上恒成立.
因此 ,
,
 .
.
解得-1≤a< ,
,
故实数a的取值范围是-1≤a< .
.
点评:本题主要考查复合函数的单调性,要注意函数的定义域及复合函数单调性的结论:同增异减的应用.

分析:用复合函数的单调性来求解,令g(x)=x2-ax-a.由“f(x)=log
 g(x)在(-∞,-
g(x)在(-∞,- )上为增函数”,可知g(x)应在(-∞,-
)上为增函数”,可知g(x)应在(-∞,- )上为减函数且g(x)>0在(-∞,-
)上为减函数且g(x)>0在(-∞,- )上恒成立.再用“对称轴在区间的右侧,且最小值大于零”求解可得结果.
)上恒成立.再用“对称轴在区间的右侧,且最小值大于零”求解可得结果.解答:令g(x)=x2-ax-a.
∵f(x)=log
 g(x)在(-∞,-
g(x)在(-∞,- )上为增函数,
)上为增函数,∴g(x)应在(-∞,-
 )上为减函数且g(x)>0
)上为减函数且g(x)>0在(-∞,-
 )上恒成立.
)上恒成立.因此
 ,
, .
.解得-1≤a<
 ,
,故实数a的取值范围是-1≤a<
 .
.点评:本题主要考查复合函数的单调性,要注意函数的定义域及复合函数单调性的结论:同增异减的应用.

练习册系列答案
相关题目
 在区间
在区间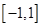 上是增函数.
上是增函数. 的值组成的集合
的值组成的集合 ;
; 的方程
的方程 的两个非零实根为
的两个非零实根为 、
、 .试问:是否存在实数
.试问:是否存在实数 ,使得不等式
,使得不等式 对任意
对任意 及
及 恒成立?若存在,求
恒成立?若存在,求 在区间
在区间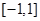 上是增函数,则
上是增函数,则 的取值范围为(
)
的取值范围为(
)  B、
B、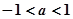
 D、不存在
D、不存在 在区间
在区间 上是增函数.
上是增函数. 的值组成的集合
的值组成的集合 ;
; 的方程
的方程 的两个非零实根为
的两个非零实根为 ,试问:是否存在实数
,试问:是否存在实数 ,使得不等式
,使得不等式 对任意
对任意 及
及 恒成立?若存在,求
恒成立?若存在,求 在区间
在区间 上是增函数,则实数
上是增函数,则实数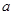 的范围是( )
的范围是( ) B.
B.  C.
C.  D.
D. 