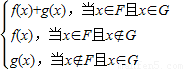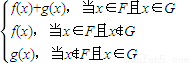题目内容
对定义域分别是F,G的函数y=f(x),y=g(x),规定:
函数
已知函数f(x)=x2,g(x)=alnx(a∈R)。
(1)求函数h(x)的解析式;
(2)对于实数a,函数h(x)是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由。
函数

已知函数f(x)=x2,g(x)=alnx(a∈R)。
(1)求函数h(x)的解析式;
(2)对于实数a,函数h(x)是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由。
解:(1)因为函数f(x)=x2的定义域F=(-∞,+∞),
函数g(x)=alnx的定义域G=(0,+∞),
所以 ;
;
(2)当x≤0时,函数h(x)=x2单调递减,
所以函数h(x)在(-∞,0]上的最小值为h(0)=0
当x>0时,h(x)=x2+alnx
若a=0,函数h(x)=x2在(0,+∞)上单调递增,此时,函数h(x)不存在最小值
若a>0,因为h'(x)=
所以函数h(x)=x2+alnx在(0,+∞)上单调递增,
此时,函数h(x)不存在最小值,
若a<0,因为h'(x)=
所以函数h(x)=x2+alnx在上单调递减,在 上单调递增
上单调递增
此时,函数h(x)的最小值为
因为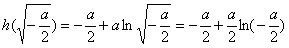

所以当-2e≤a<0时,
当a<-2e时,
综上可知,当a>0时,函数h(x)没有最小值;
当-2e≤a≤0时,函数h(x)的最小值为h(0)=0;
当a<-2e时,函数h(x)的最小值为
 。
。
函数g(x)=alnx的定义域G=(0,+∞),
所以
 ;
;(2)当x≤0时,函数h(x)=x2单调递减,
所以函数h(x)在(-∞,0]上的最小值为h(0)=0
当x>0时,h(x)=x2+alnx
若a=0,函数h(x)=x2在(0,+∞)上单调递增,此时,函数h(x)不存在最小值
若a>0,因为h'(x)=

所以函数h(x)=x2+alnx在(0,+∞)上单调递增,
此时,函数h(x)不存在最小值,
若a<0,因为h'(x)=

所以函数h(x)=x2+alnx在上单调递减,在
 上单调递增
上单调递增此时,函数h(x)的最小值为

因为
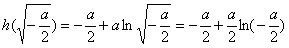

所以当-2e≤a<0时,

当a<-2e时,

综上可知,当a>0时,函数h(x)没有最小值;
当-2e≤a≤0时,函数h(x)的最小值为h(0)=0;
当a<-2e时,函数h(x)的最小值为
 。
。
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目