题目内容
9. 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.(1)求平面PAB与平面PCD所成二面角的余弦值;
(2)点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.
分析 以A为坐标原点,以AB、AD、AP所在直线分别为x、y、z轴建系A-xyz.
(1)所求值即为平面PAB的一个法向量与平面PCD的法向量的夹角的余弦值的绝对值,计算即可;
(2)利用换元法可得cos2<$\overrightarrow{CQ}$,$\overrightarrow{DP}$>≤$\frac{9}{10}$,结合函数y=cosx在(0,$\frac{π}{2}$)上的单调性,计算即得结论.
解答 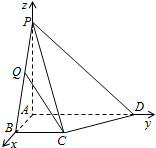 解:以A为坐标原点,以AB、AD、AP所在直线分别为x、y、z轴建系A-xyz如图,
解:以A为坐标原点,以AB、AD、AP所在直线分别为x、y、z轴建系A-xyz如图,
由题可知B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).
(1)∵AD⊥平面PAB,∴$\overrightarrow{AD}$=(0,2,0),是平面PAB的一个法向量,
∵$\overrightarrow{PC}$=(1,1,-2),$\overrightarrow{PD}$=(0,2,-2),
设平面PCD的法向量为$\overrightarrow{m}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PC}=0}\\{\overrightarrow{m}•\overrightarrow{PD}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x+y-2z=0}\\{2y-2z=0}\end{array}\right.$,
取y=1,得$\overrightarrow{m}$=(1,1,1),
∴cos<$\overrightarrow{AD}$,$\overrightarrow{m}$>=$\frac{\overrightarrow{AD}•\overrightarrow{m}}{|\overrightarrow{AD}||\overrightarrow{m}|}$=$\frac{\sqrt{3}}{3}$,
∴平面PAB与平面PCD所成两面角的余弦值为$\frac{\sqrt{3}}{3}$;
(2)∵$\overrightarrow{BP}$=(-1,0,2),设$\overrightarrow{BQ}$=λ$\overrightarrow{BP}$=(-λ,0,2λ)(0≤λ≤1),
又$\overrightarrow{CB}$=(0,-1,0),则$\overrightarrow{CQ}$=$\overrightarrow{CB}$+$\overrightarrow{BQ}$=(-λ,-1,2λ),
又$\overrightarrow{DP}$=(0,-2,2),从而cos<$\overrightarrow{CQ}$,$\overrightarrow{DP}$>=$\frac{\overrightarrow{CQ}•\overrightarrow{DP}}{|\overrightarrow{CQ}||\overrightarrow{DP}|}$=$\frac{1+2λ}{\sqrt{2+10{λ}^{2}}}$,
设1+2λ=t,t∈[1,3],
则cos2<$\overrightarrow{CQ}$,$\overrightarrow{DP}$>=$\frac{2{t}^{2}}{5{t}^{2}-10t+9}$=$\frac{2}{9(\frac{1}{t}{-\frac{5}{9})}^{2}+\frac{20}{9}}$≤$\frac{9}{10}$,
当且仅当t=$\frac{9}{5}$,即λ=$\frac{2}{5}$时,|cos<$\overrightarrow{CQ}$,$\overrightarrow{DP}$>|的最大值为$\frac{3\sqrt{10}}{10}$,
因为y=cosx在(0,$\frac{π}{2}$)上是减函数,此时直线CQ与DP所成角取得最小值.
又∵BP=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,∴BQ=$\frac{2}{5}$BP=$\frac{2\sqrt{5}}{5}$.
点评 本题考查求二面角的三角函数值,考查用空间向量解决问题的能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{6}$ |
 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形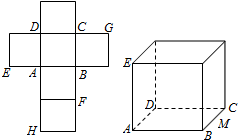 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.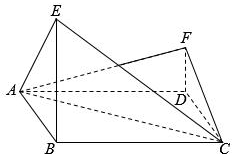 如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.