题目内容
有11名学生,其中女生3名,男生8名,从中选出5名学生组成代表队,要求至少有1名女生参加,则不同的选派方法种数是 ( )
| A．406 | B．560 | C．462 | D．154 |
A
解析试题分析：根据题意，由于将所有的学生中抽取5名，所有的情况有
,而其中没有女生的情况有
，则可知从中选出5名学生组成代表队,要求至少有1名女生参加,则不同的选派方法种数462-56=406，故选A.
考点：排列组合的运用
点评：本题考查组合的运用，对于“至少或至多有一个”一类的问题，一般用间接法
练习册系列答案
相关题目
从0，1，2，3，4，5六个数中任取四个互异的数字组成四位数，个位，百位上必排偶数数字的四位数共有（ ）
| A．52个 | B．60个 | C．54 | D．66个 |
在
的展开式中，
的系数是
A． | B． | C． | D． |
若
展开式中存在常数项，则n的最小值为( )
| A．５ | B．６ | C．７ | D．８ |
由
，
，
，
组成没有重复数字的三位数，其中奇数的个数为（ ）
| A．36 | B．24 | C．12 | D．6 |
有一排7只发光二极管，每只二极管点亮时可发出红光或绿光，若每次恰有3只二极管点亮，且相邻的两只不能同时点亮，根据三只点亮的不同位置，或不同颜色来表示不同的信息，则这排二极管能表示的信息种数共有（ ）种
| A．10 | B．48 | C．60 | D．80 |
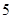个人排成一排，其中甲、乙两人至少有一人在两端的排法种数有（ ）
A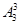． | B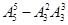． | C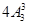． | D． |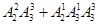
将一个三位数的三个数字顺序颠倒，将所得到的数和原数相加，若和中没有一个数字是偶数，则称这个数是奇和数。那么，所有的三位数中，奇和数有（ ）
| A．80 | B．100 | C．120 | D．160 |
若
展开式各项系数和为256，设
为虚数单位，复数
的运算结果为（ ）
| A．4 | B．-4 | C．2 | D．-2 |