题目内容
 如图,点F为椭圆
如图,点F为椭圆 =1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为
=1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为
- A.

- B.

- C.

- D.

B
分析:设线段PF的中点为M,另一个焦点F′,利用OM是△FPF′的中位线,以及椭圆的定义求出直角三角形OMF的三边之长,使用勾股定理求离心率.
解答:设线段PF的中点为M,另一个焦点F′,由题意知,OM=b,又OM是△FPF′的中位线,
∴OM= PF′=b,PF′=2b,由椭圆的定义知 PF=2a-PF′=2a-2b,
PF′=b,PF′=2b,由椭圆的定义知 PF=2a-PF′=2a-2b,
又 MF= PF=
PF= (2a-2b)=a-b,又OF=c,
(2a-2b)=a-b,又OF=c,
直角三角形OMF中,由勾股定理得:(a-b)2+b2=c2,又a2-b2=c2,
可求得离心率 e= =
= ,故答案选 B.
,故答案选 B.
点评:本题考查椭圆的定义,椭圆上任一点到两个焦点的距离之和等于常数2a.
分析:设线段PF的中点为M,另一个焦点F′,利用OM是△FPF′的中位线,以及椭圆的定义求出直角三角形OMF的三边之长,使用勾股定理求离心率.
解答:设线段PF的中点为M,另一个焦点F′,由题意知,OM=b,又OM是△FPF′的中位线,
∴OM=
 PF′=b,PF′=2b,由椭圆的定义知 PF=2a-PF′=2a-2b,
PF′=b,PF′=2b,由椭圆的定义知 PF=2a-PF′=2a-2b,又 MF=
 PF=
PF= (2a-2b)=a-b,又OF=c,
(2a-2b)=a-b,又OF=c,直角三角形OMF中,由勾股定理得:(a-b)2+b2=c2,又a2-b2=c2,
可求得离心率 e=
 =
= ,故答案选 B.
,故答案选 B.点评:本题考查椭圆的定义,椭圆上任一点到两个焦点的距离之和等于常数2a.

练习册系列答案
相关题目
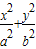 =1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
=1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )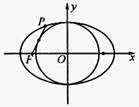

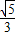
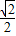

 =1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
=1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )




 =1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
=1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )




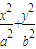 =1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
=1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )

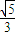
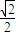

 =1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
=1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )



