题目内容
设 满足约束条件
满足约束条件 ,若目标函数z=ax+by(a>0,b>0)的最大值为8,则ab的最大值为( )
,若目标函数z=ax+by(a>0,b>0)的最大值为8,则ab的最大值为( )
| A.4 | B.5 | C.7 | D.8 |
A
解析
如图为满足条件的可行域
因为a>0,b>0,所以在点(1,4)处,目标函数z=ax+by有最大值z=a+4b
∴a+4b=8
∵ab= (4ab)≤
(4ab)≤
 =
= ×42=4
×42=4
等号当且仅当a=4b,即a=4,b=1时成立
ab的最大值为4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若变量 、
、 满足约束条件
满足约束条件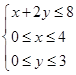 ,则
,则 的最大值等于( )
的最大值等于( )
A. | B.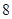 | C. | D.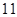 |
设 其中实数
其中实数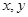 满足
满足 ,若
,若 的最大值为
的最大值为 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
(2011•湖北)已知向量 =(x+z,3),
=(x+z,3), =(2,y﹣z),且
=(2,y﹣z),且 ⊥
⊥ ,若x,y满足不等式|x|+|y|≤1,则z的取值范围为( )
,若x,y满足不等式|x|+|y|≤1,则z的取值范围为( )
| A.[﹣2,2] | B.[﹣2,3] | C.[﹣3,2] | D.[﹣3,3] |
(2013•天津)设变量x,y满足约束条件 ,则目标函数z=y﹣2x的最小值为( )
,则目标函数z=y﹣2x的最小值为( )
| A.﹣7 | B.﹣4 | C.1 | D.2 |
若集合P={0,1,2},Q={(x,y)|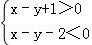 ,x,y∈P},则Q中元素的个数是( )
,x,y∈P},则Q中元素的个数是( )
| A.3 | B.5 | C.7 | D.9 |
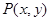 使关于t的二次方程
使关于t的二次方程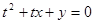 的根都是绝对值不超过1的实数,那么这样的点
的根都是绝对值不超过1的实数,那么这样的点 的集合在平面内的区域的形状是( )
的集合在平面内的区域的形状是( )
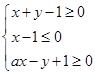 (a为常数)所表示的平面区域的面积等于2,则a的值为( )
(a为常数)所表示的平面区域的面积等于2,则a的值为( ) (其中e为自然对数的底数)在点(0,1)处的切线与直线y=-x+3和x轴所围成的区域为D(包含边界),点P(x,y)为区域D内的动点,则z=x-3y的最大值为( )
(其中e为自然对数的底数)在点(0,1)处的切线与直线y=-x+3和x轴所围成的区域为D(包含边界),点P(x,y)为区域D内的动点,则z=x-3y的最大值为( )