题目内容
给出下列命题:①“ ”是“
”是“ ”的充要条件;②“
”的充要条件;②“ ”是“
”是“ ”的充分不必要条件;③若O为坐标原点,点A的坐标为(2,-3),
”的充分不必要条件;③若O为坐标原点,点A的坐标为(2,-3), ,则△OAB一定是等腰直角三角形其中正确命题的个数是( )
,则△OAB一定是等腰直角三角形其中正确命题的个数是( )A.0
B.1
C.2
D.3
【答案】分析:通过举反例可得①、②不正确,设点B的坐标,由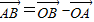 ,用待定系数法求出点B的坐标,根据向量的模的定义求出
,用待定系数法求出点B的坐标,根据向量的模的定义求出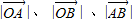 的值,由勾股定理可得△OAB是等腰直角三角形,从而得到③正确.
的值,由勾股定理可得△OAB是等腰直角三角形,从而得到③正确.
解答:解:①不正确,当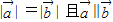 时,不一定有
时,不一定有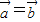 ,也有可能
,也有可能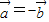 .
.
②不正确,因为当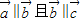 时,若
时,若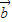 =
=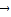 ,则不能推出
,则不能推出 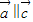 ,故充分性不成立.
,故充分性不成立.
③正确,设点B(m,n ),由于O为坐标原点,点A的坐标为(2,-3),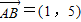 ,
,
则由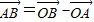 得 n+3=5,m-2=1,∴m=3,n=2,∴B(3,2).
得 n+3=5,m-2=1,∴m=3,n=2,∴B(3,2).
∴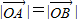 =
=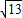 ,
,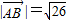 ,∴△OAB是等腰直角三角形.
,∴△OAB是等腰直角三角形.
故选:B.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,两个向量相等或相反,判断三角形的形状,充分条件、必要条件、充要条件的定义,准确理解向量的有关定义和性质是解题的关键.通过举反例来说明某个命题不正确,是一种简单有效的方法.
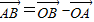 ,用待定系数法求出点B的坐标,根据向量的模的定义求出
,用待定系数法求出点B的坐标,根据向量的模的定义求出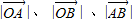 的值,由勾股定理可得△OAB是等腰直角三角形,从而得到③正确.
的值,由勾股定理可得△OAB是等腰直角三角形,从而得到③正确.解答:解:①不正确,当
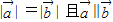 时,不一定有
时,不一定有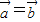 ,也有可能
,也有可能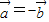 .
.②不正确,因为当
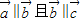 时,若
时,若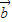 =
=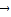 ,则不能推出
,则不能推出 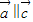 ,故充分性不成立.
,故充分性不成立.③正确,设点B(m,n ),由于O为坐标原点,点A的坐标为(2,-3),
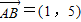 ,
,则由
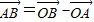 得 n+3=5,m-2=1,∴m=3,n=2,∴B(3,2).
得 n+3=5,m-2=1,∴m=3,n=2,∴B(3,2).∴
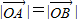 =
=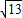 ,
,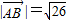 ,∴△OAB是等腰直角三角形.
,∴△OAB是等腰直角三角形.故选:B.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,两个向量相等或相反,判断三角形的形状,充分条件、必要条件、充要条件的定义,准确理解向量的有关定义和性质是解题的关键.通过举反例来说明某个命题不正确,是一种简单有效的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目