题目内容
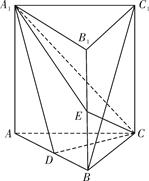
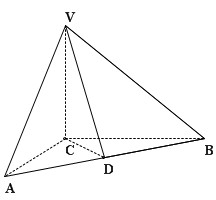
如图,在三棱锥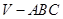 中,
中,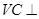 底面
底面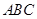 ,
, 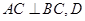 为
为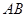 的中点,
的中点,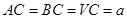 .
.
(1)求证: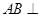 平面
平面 ;
;
(2)求点 到平面
到平面 的距离。
的距离。
(1)证明过程详见解析;(2)点 到平面
到平面 的距离为
的距离为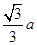 .
.
解析试题分析:本题以三棱锥为几何背景考查线面垂直的判断和点到面的距离的求法,可以运用传统几何法求解,突出考查空间想象能力和计算能力.第一问,先利用线面垂直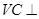 平面
平面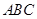 ,得到线线垂直
,得到线线垂直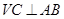 ,由等腰三角形,得
,由等腰三角形,得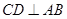 ,由上述两个条件得
,由上述两个条件得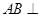 平面
平面 ;第二问,利用第一问可得面
;第二问,利用第一问可得面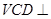 面
面 ,利用面面垂直的性质,得
,利用面面垂直的性质,得 到
到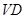 的距离即为
的距离即为 到面
到面 的距离,在直角三角形
的距离,在直角三角形 中,用等面积法表示
中,用等面积法表示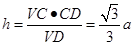 .法二:第二问,等体积法求点面距离,
.法二:第二问,等体积法求点面距离, ,即
,即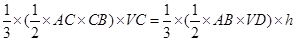 ,得
,得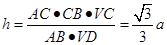 .
.
试题解析:(1)因为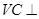 平面
平面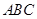 ,
, 平面
平面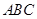 ,
,
所以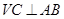 2分
2分
又因为在 中,
中,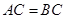 ,
,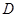 为
为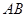 的中点,
的中点,
所以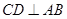 4分
4分
又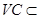 平面
平面 ,
,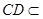 平面
平面 ,且
,且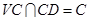 ,
,
所以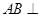 平面
平面 6分
6分
(2)法一:因为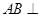 平面
平面 且
且 平面
平面
所以平面
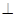 平面
平面 , 8分
, 8分
又因为平面
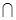 平面
平面
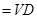 ,
,
所以点 到
到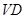 的距离
的距离 即为点
即为点 到平面
到平面 的距离, 10分
的距离, 10分
在直角三角形 中,由
中,由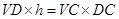 11分
11分
得 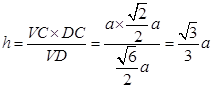 13分
13分
所以点 到平面
到平面 的距离为
的距离为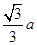 . 14分
. 14分
法二:设点 到平面
到平面 的距离为
的距离为 , 据
, 据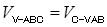 8分
8分
即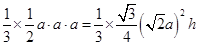 ,得
,得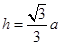 13分
13分
所以点 到平面
到平面 的距离为
的距离为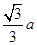 . 14分
. 14分
考点:1.线面垂直的判定定理;2.面面垂直的性质;3.等体

练习册系列答案
相关题目
 中,底面△
中,底面△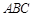 为等腰直角三角形,
为等腰直角三角形,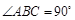 ,
, 为棱
为棱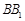 上一点,且平面
上一点,且平面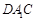 ⊥平面
⊥平面 .
.
 为何值时,二面角
为何值时,二面角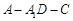 的平面角为
的平面角为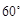 .
.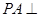 平面
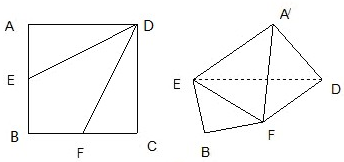
平面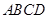 ,四边形
,四边形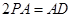 ,
,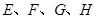 分别是线段
分别是线段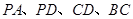 的中点.
的中点.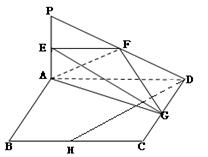
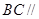 平面
平面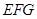 ;
;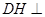 平面
平面 ;
;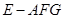 与四棱锥
与四棱锥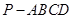 的体积比.
的体积比. .
.
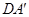 ⊥EF;
⊥EF;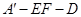 的平面角的余弦值.
的平面角的余弦值.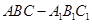 中,侧面
中,侧面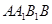 ⊥底面
⊥底面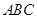 ,侧棱
,侧棱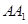 与底面
与底面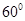 的角,
的角,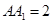 .底面
.底面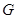 点,
点,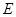 是线段
是线段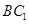 上一点,且
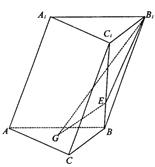
上一点,且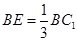 .
.
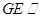 //侧面
//侧面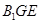 与底面
与底面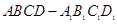 中,
中,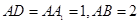 ,点E是AB的中点.
,点E是AB的中点.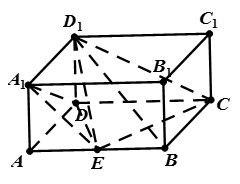
 平面
平面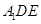 ;
;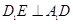 ;
;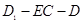 的正切值.
的正切值.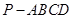 中,平面
中,平面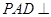 平面
平面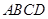 ,
,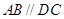 ,
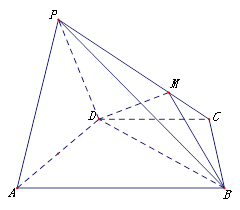
,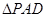 是等边三角形,已知
是等边三角形,已知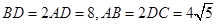 .
.
 是
是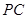 上的一点,证明:平面
上的一点,证明:平面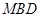 ;
;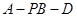 的余弦值.
的余弦值.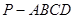 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱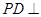 底面ABCD,
底面ABCD,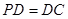 ,E是PC的中点.
,E是PC的中点.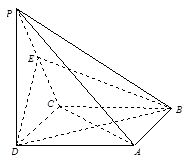
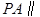 平面EDB;
平面EDB;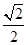 AB.
AB.