题目内容
 如图,底面为平行四边形的四棱柱ABCD-A′B′C′D′,DD′⊥底面ABCD,∠DAB=60°,AB=2AD,DD′=3AD,E、F分别是AB、D′E的中点.
如图,底面为平行四边形的四棱柱ABCD-A′B′C′D′,DD′⊥底面ABCD,∠DAB=60°,AB=2AD,DD′=3AD,E、F分别是AB、D′E的中点.(Ⅰ)求证:DF⊥CE;
(Ⅱ)求二面角A-EF-C的余弦值.
分析:(Ⅰ)证明CE⊥DE,CE⊥DD′,从而可得CE⊥平面DD′E,进而可得CE⊥DF;
(Ⅱ)取AE中点H,分别以DH、DC、DD'所在直线为x、y、z轴建立空间直角坐标系,用坐标表示点与向量,求得平面AEF的法向量
=(2
,0,1),平面CEF的法向量
=(3
,3,2),利用向量夹角公式,即可求得二面角A-EF-C的余弦值.
(Ⅱ)取AE中点H,分别以DH、DC、DD'所在直线为x、y、z轴建立空间直角坐标系,用坐标表示点与向量,求得平面AEF的法向量
| n1 |
| 3 |
| n2 |
| 3 |
解答: (Ⅰ)证明:∵AD=AE,∠DAE=60°∴△DAE为等边三角形,
(Ⅰ)证明:∵AD=AE,∠DAE=60°∴△DAE为等边三角形,
设AD=1,则DE=1,CE=
,CD=2,∴∠DEC=90°,
即CE⊥DE. …(3分)
∵DD'⊥底面ABCD,CE?平面ABCD,∴CE⊥DD′.
∵DE∩DD′=D
∴CE⊥平面DD′E
∵DF?平面DD′E
∴CE⊥DF. …(6分)
(Ⅱ)解:取AE中点H,则AD=AE=
AB,
又∠DAE=60°,所以△DAE为等边三角形,则DH⊥AB,DH⊥CD.
分别以DH、DC、DD'所在直线为x、y、z轴建立空间直角坐标系,
设AD=1,则D(0,0,0),E(
,
,0),A(
,-
,0),D′(0,0,3),F(
,
,
),C(0,2,0).
=(-
,-
,
),
=(0,1,0),
=(
,-
,0).
设平面AEF的法向量为
=(x,y,z),则
,取
=(2
,0,1). …(10分)
平面CEF的法向量为
=(x,y,z),则
,取
=(3
,3,2). …(12分)
∴cosα<
,
>=
=
=
.
∵二面角A-EF-C为钝二面角
∴二面角A-EF-C的余弦值为-
. …(15分)
 (Ⅰ)证明:∵AD=AE,∠DAE=60°∴△DAE为等边三角形,
(Ⅰ)证明:∵AD=AE,∠DAE=60°∴△DAE为等边三角形,设AD=1,则DE=1,CE=
| 3 |
即CE⊥DE. …(3分)
∵DD'⊥底面ABCD,CE?平面ABCD,∴CE⊥DD′.
∵DE∩DD′=D
∴CE⊥平面DD′E
∵DF?平面DD′E
∴CE⊥DF. …(6分)
(Ⅱ)解:取AE中点H,则AD=AE=
| 1 |
| 2 |
又∠DAE=60°,所以△DAE为等边三角形,则DH⊥AB,DH⊥CD.
分别以DH、DC、DD'所在直线为x、y、z轴建立空间直角坐标系,
设AD=1,则D(0,0,0),E(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| EF |
| ||
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| AE |
| CE |
| ||
| 2 |
| 3 |
| 2 |
设平面AEF的法向量为
| n1 |
|
| n1 |
| 3 |
平面CEF的法向量为
| n2 |
|
| n2 |
| 3 |
∴cosα<
| n1 |
| n2 |
|
| ||||
|
|
| 20 | ||||
|
| ||
| 13 |
∵二面角A-EF-C为钝二面角
∴二面角A-EF-C的余弦值为-
| ||
| 13 |
点评:本题考查线面垂直、线线垂直、考查面面角,解题的关键是掌握线面垂直的判定,正确求出平面的法向量,属于中档题.

练习册系列答案
相关题目
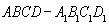

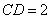
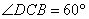
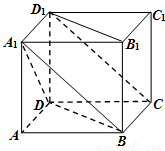
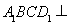
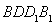
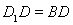
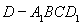
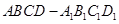 中,
中,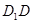
 底面
底面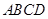 ,
,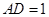 ,
,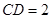 ,
,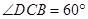 .
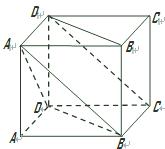
.
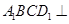 平面
平面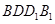 ;
;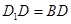 ,求四棱锥
,求四棱锥 的体积.
的体积. 中,
中,
 底面
底面 ,
, ,
, ,
, .
. 平面
平面 ;
; ,求四棱锥
,求四棱锥 的体积.
的体积.
 中,
中, ,
, 平面
平面 ,且
,且 ,点
,点 是
是 的中点.
的中点. 平面
平面 ;
;  平面
平面
