Question

（12分）

已知数列{a_n}满足a₁=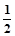，且前n项和S_n满足：S_n=n²a_n，求a₂,a₃,a₄,猜想{a_n}的通项公式，并加以证明。

 

Answer 1

【答案】

见解析

【解析】利用数列的前n项公式即可求出数列的前4项，根据前4项归纳出数列的通项，然后再根据数学归纳法的步骤证明猜想成立

解：由S 得  a

由a

由此猜想a下面用数学归纳法证明

(1)n=1 a命题成立

(2)假设n=k时命题成立，即a

那么当n=k+1时，S  S  则 S

即a

a  所以：a

a 即 n=k+1时命题成立。

由（1）（2）知对一切n命题成立。