题目内容
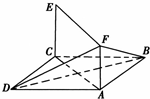 如图所示,已知平行四边形ABCD和平行四边形ACEF所在的平面相交于直线AC,EC⊥平面ABCD,AB=1,AD=2,ADC=60°,AF=
如图所示,已知平行四边形ABCD和平行四边形ACEF所在的平面相交于直线AC,EC⊥平面ABCD,AB=1,AD=2,ADC=60°,AF=| 3 |
(1)求证:AC⊥BF;
(2)求二面角F-BD-A的余弦值.
分析:(1)要证线线垂直,只需要证明线面垂直,即证AC⊥平面ABF,再利用线面垂直的判定,即可证得;
(2)建立空间直角坐标系,求出平面ABD的一个法向量、平面FBD的法向量,利用向量的夹角公式,即可求二面角F-BD-A的余弦值.
(2)建立空间直角坐标系,求出平面ABD的一个法向量、平面FBD的法向量,利用向量的夹角公式,即可求二面角F-BD-A的余弦值.
解答:(1)证明:∵AB=1,BC=AD=2,∠ADC=60°,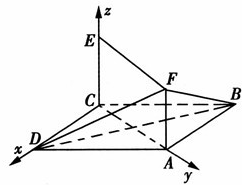
∴AC2=1+4-2×1×2×cos60°=3
∴AC=
,
又∵AB=1,BC=2
∴∠BAC=∠ACD=90°,
∴AC⊥AB
又AF⊥AC,AB∩AF=A
∴AC⊥平面ABF,
又∵BF?平面ABF,
∴AC⊥BF;
(2)解:建立如图所示的坐标系,则C(0,0,0),D(1,0,0),A(0,
,0),F(0,
,
),B(-1,
,0)
平面ABD的一个法向量
=(0,0,1),
设平面FBD的法向量为
=(x,y,z)
∵
=(-1,
,
),
=(-2,
,0),
由
,可得
令z=1,得
=(-
,-2,1)为平面FBD的一个法向量.
∴cos<
,
>=
=
故所求二面角F-BD-A的余弦值为
.

∴AC2=1+4-2×1×2×cos60°=3
∴AC=
| 3 |
又∵AB=1,BC=2
∴∠BAC=∠ACD=90°,
∴AC⊥AB
又AF⊥AC,AB∩AF=A
∴AC⊥平面ABF,
又∵BF?平面ABF,
∴AC⊥BF;
(2)解:建立如图所示的坐标系,则C(0,0,0),D(1,0,0),A(0,
| 3 |
| 3 |
| 3 |
| 3 |
平面ABD的一个法向量
| n |
设平面FBD的法向量为
| m |
∵
| DF |
| 3 |
| 3 |
| DB |
| 3 |
由
|
|
令z=1,得
| m |
| 3 |
∴cos<
| m |
| n |
| ||||
|
|
| ||
| 4 |
故所求二面角F-BD-A的余弦值为
| ||
| 4 |
点评:本题重点考查线面垂直的判定与性质,考查面面角,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
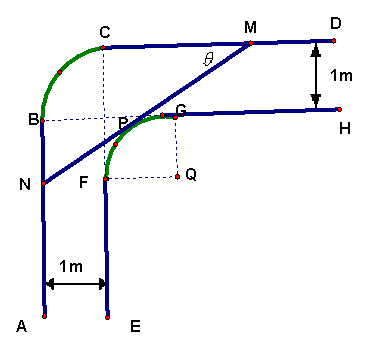
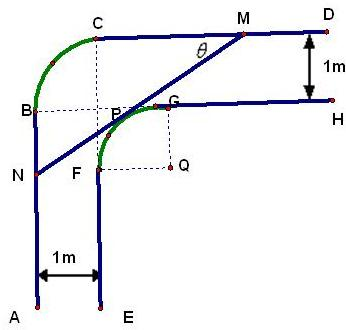 一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m. 一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.