题目内容
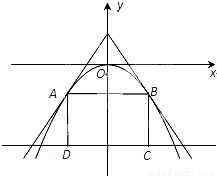
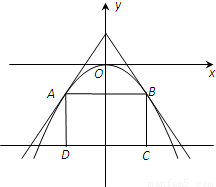
如图,过点(0,a3)的两直线与抛物线y=-ax2相切于A、B两点,AD、BC垂直于直线y=-8,垂足分别为D、C.
(1)若a=1,求矩形ABCD面积;
(2)若a∈(0,2),求矩形ABCD面积的最大值.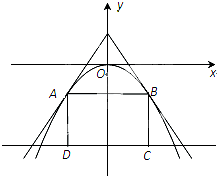
(1)若a=1,求矩形ABCD面积;
(2)若a∈(0,2),求矩形ABCD面积的最大值.

(1)设切点为(x0,y0),则y0=-ax02,
因为y'=-2ax,所以切线方程为y-y0=-2ax0(x-x0),即y+ax02=-2ax0(x-x0),
因为切线过点(0,a3),所以a3+ax02=-2ax0(0-x0),即a3=ax02,于是x0=±a.
将x0=±a代入y0=-ax02得y0=-a3.
所以AB=2a,BC=8-a3,所以矩形ABCD面积为S=16a-2a4,
当a=1时,矩形ABCD的面积S=16×1-2×14=14;
(2)由(1)得:矩形ABCD面积为S=16a-2a4(0<a<2),
则S'=16-8a3=8(2-a3).
所以当0<a<
时,S'>0;当
<a<2时,S'<0;
故当a=
时,S有最大值为S=16×
-2×(
)4=12
.
因为y'=-2ax,所以切线方程为y-y0=-2ax0(x-x0),即y+ax02=-2ax0(x-x0),
因为切线过点(0,a3),所以a3+ax02=-2ax0(0-x0),即a3=ax02,于是x0=±a.
将x0=±a代入y0=-ax02得y0=-a3.
所以AB=2a,BC=8-a3,所以矩形ABCD面积为S=16a-2a4,
当a=1时,矩形ABCD的面积S=16×1-2×14=14;
(2)由(1)得:矩形ABCD面积为S=16a-2a4(0<a<2),
则S'=16-8a3=8(2-a3).
所以当0<a<
| 3 | 2 |
| 3 | 2 |
故当a=
| 3 | 2 |
| 3 | 2 |
| 3 | 2 |
| 3 | 2 |

练习册系列答案
相关题目
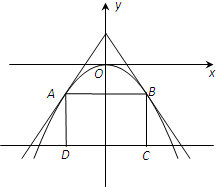 如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.
如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值. 如图,过点(0,a3)的两直线与抛物线y=-ax2相切于A、B两点,AD、BC垂直于直线y=-8,垂足分别为D、C.
如图,过点(0,a3)的两直线与抛物线y=-ax2相切于A、B两点,AD、BC垂直于直线y=-8,垂足分别为D、C.