题目内容
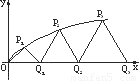
设P1,P2,P3,…Pn,是曲线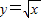 上的点列,Q1,Q2,Q3,…Qn是x轴的正半轴上的点列,O为坐标原点,且△OQ1P1,△Q1Q2P2,…,△QnQn+1Pn+1是等边三角形,设它们的边长分别为a1,a2,a3,…an,求{an}前n项和Sn.
上的点列,Q1,Q2,Q3,…Qn是x轴的正半轴上的点列,O为坐标原点,且△OQ1P1,△Q1Q2P2,…,△QnQn+1Pn+1是等边三角形,设它们的边长分别为a1,a2,a3,…an,求{an}前n项和Sn.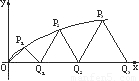
【答案】分析:当n=1时,由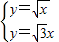 ,得
,得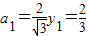 ,令Sn=a1+a2+…+an,由△Qn-1PnQn为正三角形知
,令Sn=a1+a2+…+an,由△Qn-1PnQn为正三角形知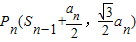 ,由点Pn在曲线
,由点Pn在曲线 上,知即
上,知即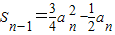 ,由此入手能够求出{an}前n项和Sn.
,由此入手能够求出{an}前n项和Sn.
解答:解:当n=1时,由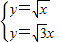 ,得
,得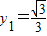 ,
,
∴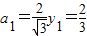 ,令Sn=a1+a2+…+an,
,令Sn=a1+a2+…+an,
则由△Qn-1PnQn为正三角形,(Q为原点,S=0),
∴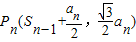 ,
,
又由点Pn在曲线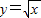 上,
上,
∴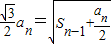 ,
,
即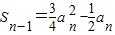
∴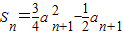 .
.
两式相减,得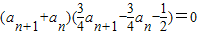 ,
,
∵an+1+an≠0,
∴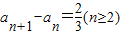
可验证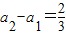 ,
,
故数列{an}是以 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,
∴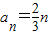 ,
,
∴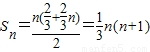 .
.
点评:本题考查等差数列的性质和函数的综合运用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.具有一定的难度,容易出错.解题时要认真审题,仔细解答.
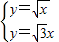 ,得
,得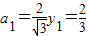 ,令Sn=a1+a2+…+an,由△Qn-1PnQn为正三角形知
,令Sn=a1+a2+…+an,由△Qn-1PnQn为正三角形知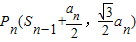 ,由点Pn在曲线
,由点Pn在曲线 上,知即
上,知即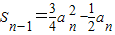 ,由此入手能够求出{an}前n项和Sn.
,由此入手能够求出{an}前n项和Sn.解答:解:当n=1时,由
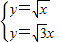 ,得
,得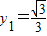 ,
,
∴
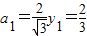 ,令Sn=a1+a2+…+an,
,令Sn=a1+a2+…+an,则由△Qn-1PnQn为正三角形,(Q为原点,S=0),
∴
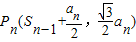 ,
,又由点Pn在曲线
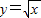 上,
上,∴
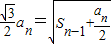 ,
,即
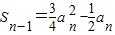
∴
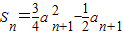 .
.两式相减,得
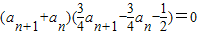 ,
,∵an+1+an≠0,
∴
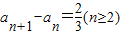
可验证
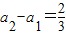 ,
,故数列{an}是以
 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,∴
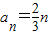 ,
,∴
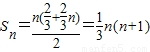 .
.点评:本题考查等差数列的性质和函数的综合运用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.具有一定的难度,容易出错.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
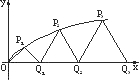 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=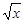 上的点列,Q1,Q2,Q3, …,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3, …,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=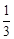 n(n+1).(13分)
n(n+1).(13分)
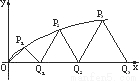 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=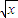 上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an= n(n+1).
n(n+1).