题目内容
(本题满分16分)
设数列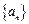 满足
满足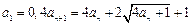 ,令
,令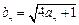 .
.
⑴试判断数列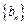 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;
⑵若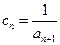 ,求
,求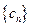 前
前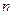 项的和
项的和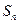 ;
;
⑶是否存在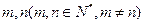 使得
使得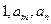 三数成等比数列?
三数成等比数列?
设数列
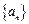 满足
满足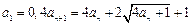 ,令
,令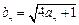 .
. ⑴试判断数列
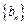 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;⑵若
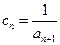 ,求
,求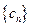 前
前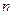 项的和
项的和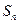 ;
;⑶是否存在
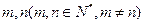 使得
使得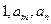 三数成等比数列?
三数成等比数列?(1)数列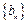 为等差数列
为等差数列
(2)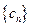 前
前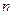 项的和
项的和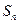
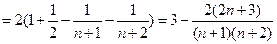
(3)不存在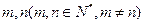 使得
使得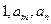 三数成等比数列.
三数成等比数列.
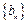 为等差数列
为等差数列(2)
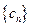 前
前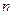 项的和
项的和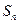
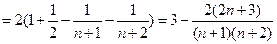
(3)不存在
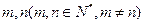 使得
使得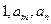 三数成等比数列.
三数成等比数列.⑴由已知得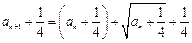 ,
,
即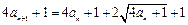 ,
,
所以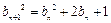 ,即
,即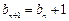 ,
,
所以数列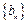 为等差数列; …………………………6分
为等差数列; …………………………6分
⑵由⑴得: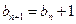 且
且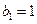 ,
,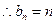 ,
,
即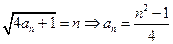 ,
,
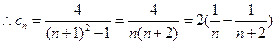 , ……………………8分
, ……………………8分
则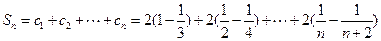
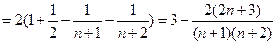 ; ………………………………10分
; ………………………………10分
⑶设存在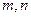 满足条件,则有
满足条件,则有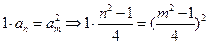 ,
,
即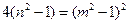 ,所以,
,所以,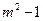 必为偶数,设为
必为偶数,设为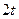 , ……………………12分
, ……………………12分
则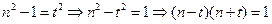 ,
,
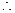 有
有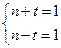 或
或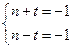 ,即
,即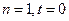 , ……………………14分
, ……………………14分
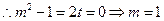 与已知矛盾.
与已知矛盾.
 不存在
不存在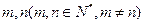 使得
使得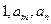 三数成等比数列.……………………16分
三数成等比数列.……………………16分
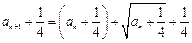 ,
, 即
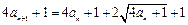 ,
, 所以
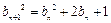 ,即
,即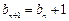 ,
, 所以数列
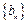 为等差数列; …………………………6分
为等差数列; …………………………6分⑵由⑴得:
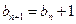 且
且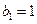 ,
,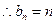 ,
,即
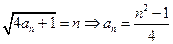 ,
,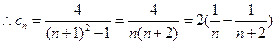 , ……………………8分
, ……………………8分则
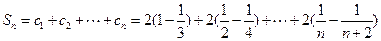
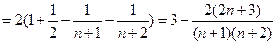 ; ………………………………10分
; ………………………………10分⑶设存在
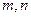 满足条件,则有
满足条件,则有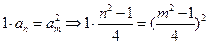 ,
,即
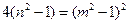 ,所以,
,所以,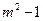 必为偶数,设为
必为偶数,设为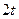 , ……………………12分
, ……………………12分则
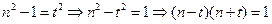 ,
,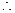 有
有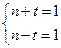 或
或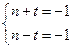 ,即
,即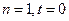 , ……………………14分
, ……………………14分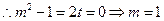 与已知矛盾.
与已知矛盾.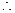 不存在
不存在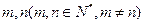 使得
使得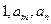 三数成等比数列.……………………16分
三数成等比数列.……………………16分
练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
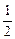 成等比数列
成等比数列
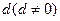
 的等差数列
的等差数列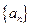 和公比为
和公比为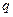 的等比数列
的等比数列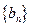 中,已知
中,已知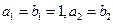 ,
,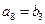 .
.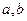 ,使
,使 得对于一切正整数
得对于一切正整数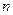 ,都有
,都有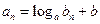 成立?若存在,求出常数
成立?若存在,求出常数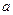 和
和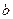 ,若不存在说明理由
,若不存在说明理由 3分)
3分) 列
列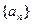 满足
满足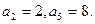
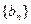 的前n项和为Tn若
的前n项和为Tn若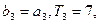 求Tn。
求Tn。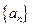 满足
满足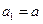 ,
,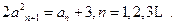
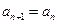 ,求
,求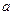 的值;
的值;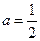 时,证明:
时,证明: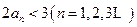 ;
;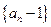 的前
的前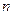 项之积为
项之积为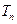 ,若对任意正整数
,若对任意正整数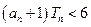 成立,求
成立,求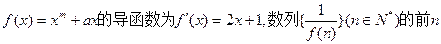 项和为
项和为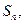 则
则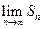 =" " ( )
=" " ( )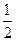
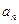 }的前n项和为
}的前n项和为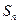 ,若
,若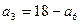 ,则
,则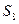 =" " ( )
=" " ( )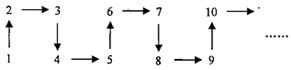
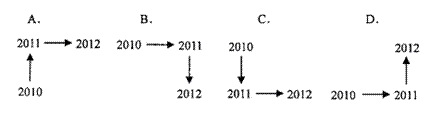
 012箭头的方向是 ( )
012箭头的方向是 ( )