题目内容
【题目】如图,已知三棱柱![]() 的侧棱垂直于底面,
的侧棱垂直于底面,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
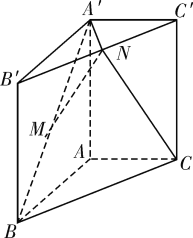
(1)证明:![]() 平面
平面![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() 平面
平面![]() ,试证明你的结论.
,试证明你的结论.
【答案】(1)见解析(2)当![]() 时,
时,![]() ⊥平面
⊥平面![]() .见解析
.见解析
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由面面平行判定定理可得平面
,由面面平行判定定理可得平面![]() ∥平面
∥平面![]() ,进而证明
,进而证明![]() 平面
平面![]() ;
;
(2)连接![]() ,可设
,可设![]() ,则
,则![]() ,要使
,要使![]() ⊥平面
⊥平面![]() ,只需
,只需![]() 即可,由线面垂直的判定定理可得
即可,由线面垂直的判定定理可得![]() 的方程,解方程即可求得
的方程,解方程即可求得![]() 的值.
的值.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() .如下图所示:
.如下图所示:

因为点![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
所以![]() N,
N,![]() ,
,
又![]()
![]() 面
面![]() ,
,![]()
![]() 面
面![]() ,
,
所以![]() ∥平面
∥平面![]() ,
,![]() ∥平面
∥平面![]() ,
,
所以平面![]() ∥平面
∥平面![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
(2)连接![]() ,如下图所示:
,如下图所示:
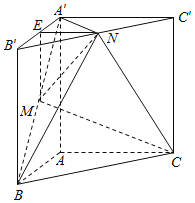
设![]() ,则
,则![]() ,
,
由题意知![]() ,
,![]() ,
,
∵三棱柱![]() 的侧棱垂直于底面,
的侧棱垂直于底面,
∴平面![]() ⊥平面
⊥平面![]() ,
,
∵![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
∴![]() ⊥平面
⊥平面![]() ,
,
∴![]() .
.
要使![]() ⊥平面
⊥平面![]() ,只需
,只需![]() 即可,
即可,
∴![]() ,
,![]() ,
,
∴ ![]() ,
,
∴当![]() 时,
时,![]() ⊥平面
⊥平面![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目

