Question

【题目】已知函数在与处都取得极值．

（1）求、的值；（2）若对时，恒成立，求实数的取值范围．

Answer 1

【答案】（1）;（2）

【解析】试题分析：（1）利用导函数求极值的方法可知 ，即可求出 ，则不难得到关于的方程组，解方程组即可求出的值；（2）要使对 时， 恒成立，则 要小于等于 在 上的最小值，根据（1）中的值，可得到函数 ，根据导函数求出函数的单调性，再根据函数 在区间 两端点的函数值，即可得到最小值，进而可得结果.

试题解析：（1）

在处都取得极值

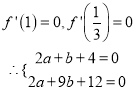即

经检验符合

（2）由（1）可知，

由 0，得的单调增区间为，由 0，得的单调减区间为∴=1是的极大值点 当时， = 4， =3++4

而- =4e-9- 所以> ，即在上的最小值为+4-3e，

要使对时， 恒成立，必须

【方法点晴】本题主要考查利用导数求函数的最值以及不等式恒成立问题，属于难题．不等式恒成立问题常见方法：① 分离参数恒成立(可)或恒成立（即可）；② 数形结合(图象在 上方即可)；③ 讨论最值或恒成立；④ 讨论参数.本题是利用方法 ① 求得 的范围.