题目内容
设函数f(x)=x2+ax+b(a、b为实常数),已知不等式|f(x)|≤|2x2+4x-6|对任意的实数x均成立.定义数列{an}和{bn}:a1=3,2an=f(an-1)+3(n=2,3,…),bn=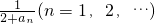 ,数列{bn}的前n项和Sn.
,数列{bn}的前n项和Sn.
(I)求a、b的值;
(II)求证: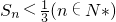 ;
;
(III )求证: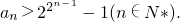
解:( I)由|f(x)|≤|2x2+4x-6|=2|(x+3)(x-1)|得f(-3)=0,f(1)=0,
故a=2,b=-3,∴f(x)=x2+2x-3
(II)由2an=f(an-1)+3=an-12+2an-1=an-1(an-1+2)(n≥2)得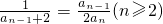 ,
,
∴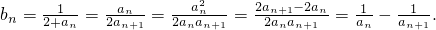
∴ =
=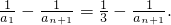
∵2an=an-12+2an-1(n≥2),∴2an-2an-1=an-12≥0(n≥2),
∴an≥an-1(n≥2),从而an≥an-1≥≥a2≥a1=3>0,即an+1>0,∴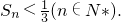
(III)由2an=an-12+2an-1(n≥2)得(an-1+1)2=2an+1<2(an+1)(n≥2),
设an+1=cn,则c1=4,且2cn>cn-12(n≥2),
于是1+log2cn>2log2cn-1(n≥2),
设dn=log2cn,则d1=2,且1+dn>2dn-1(n≥2),∴dn-1>2(dn-1-1)(n≥2),
∴dn-1>22(dn-2-1)>>2n-1(d1-1)=2n-1(n≥2),
从而n≥2时,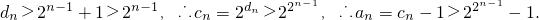
当n=1时,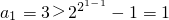 ,∴
,∴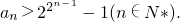
分析:( I)由|f(x)|≤|2x2+4x-6|=2|(x+3)(x-1)|知a=2,b=-3,由此可知f(x)=x2+2x-3(2分)
(II)由2an=f(an-1)+3=an-12+2an-1=an-1(an-1+2)(n≥2)知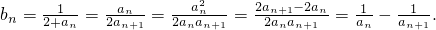 故
故 =
=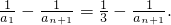 由此可知
由此可知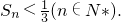
(III)由2an=an-12+2an-1(n≥2)知(an-1+1)2=2an+1<2(an+1)(n≥2),设an+1=cn,可求出1+log2cn>2log2cn-1,设dn=log2cn,可求出dn-1>22(dn-2-1)>>2n-1(d1-1)=2n-1(n≥2),由此可知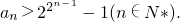
点评:本题考查数列的综合运用,难度较大,解题时要认真审题,仔细解答.
故a=2,b=-3,∴f(x)=x2+2x-3
(II)由2an=f(an-1)+3=an-12+2an-1=an-1(an-1+2)(n≥2)得
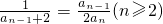 ,
,∴
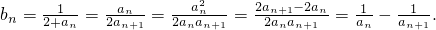
∴
 =
=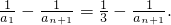
∵2an=an-12+2an-1(n≥2),∴2an-2an-1=an-12≥0(n≥2),
∴an≥an-1(n≥2),从而an≥an-1≥≥a2≥a1=3>0,即an+1>0,∴
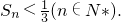
(III)由2an=an-12+2an-1(n≥2)得(an-1+1)2=2an+1<2(an+1)(n≥2),
设an+1=cn,则c1=4,且2cn>cn-12(n≥2),
于是1+log2cn>2log2cn-1(n≥2),
设dn=log2cn,则d1=2,且1+dn>2dn-1(n≥2),∴dn-1>2(dn-1-1)(n≥2),
∴dn-1>22(dn-2-1)>>2n-1(d1-1)=2n-1(n≥2),
从而n≥2时,
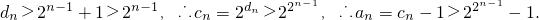
当n=1时,
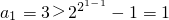 ,∴
,∴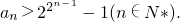
分析:( I)由|f(x)|≤|2x2+4x-6|=2|(x+3)(x-1)|知a=2,b=-3,由此可知f(x)=x2+2x-3(2分)
(II)由2an=f(an-1)+3=an-12+2an-1=an-1(an-1+2)(n≥2)知
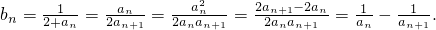 故
故 =
=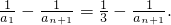 由此可知
由此可知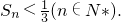
(III)由2an=an-12+2an-1(n≥2)知(an-1+1)2=2an+1<2(an+1)(n≥2),设an+1=cn,可求出1+log2cn>2log2cn-1,设dn=log2cn,可求出dn-1>22(dn-2-1)>>2n-1(d1-1)=2n-1(n≥2),由此可知
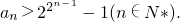
点评:本题考查数列的综合运用,难度较大,解题时要认真审题,仔细解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目