题目内容
已知数列![]() 的各项均为正数,
的各项均为正数,![]() 为其前n项和,对于任意
为其前n项和,对于任意![]() ,满足关系
,满足关系![]() 。
。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,求证:对任意正整数n,总有
,求证:对任意正整数n,总有![]() 。
。
(Ⅲ)在正数数列![]() 中,设
中,设![]() ,求数列
,求数列![]() 中的最大项。
中的最大项。
(Ⅰ)解:∵![]() ,①
,①
∴![]()
①-②,得![]()
∵![]() ,∴
,∴![]() ,
,![]()
即数列![]() 是等比数列。
是等比数列。
∴![]() ,即
,即![]() 。
。
∴![]()
![]() 。
。
(Ⅱ)证明:∵对任意正整数n,总有![]() ,
,
∴![]()
![]()
![]()
(Ⅲ)解:由![]() 知
知![]() 。
。
令![]() ,则
,则 ,
,
∵在区间![]() 上,
上,![]() ,在区间
,在区间![]() 上,
上,![]() ,
,
∴在区间![]() 上
上![]() 为单调递减函数。
为单调递减函数。
∴![]() 且
且![]() 时,
时,![]() 是递减数列。
是递减数列。
又![]() ,∴数列
,∴数列![]() 中的最大项为
中的最大项为![]() 。
。

练习册系列答案
相关题目
 的各项均为正实数,且其前
的各项均为正实数,且其前 项和
项和 满足
满足 。(1)证明:数列
。(1)证明:数列 ,求数列
,求数列 的前
的前 。
。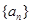 的各项均为正整数,对于
的各项均为正整数,对于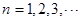 ,有
,有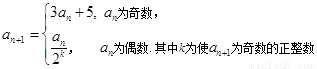 当
当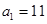 时,
时,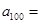 ______;
______;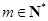 ,当
,当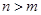 且
且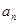 为奇数时,
为奇数时, ,则
,则
 当
当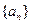 的各项均为正整数,对于
的各项均为正整数,对于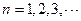 ,有
,有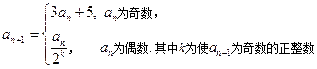 当
当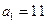 时,
时,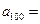 ______;
______;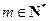 ,当
,当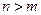 且
且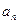 为奇数时,
为奇数时,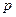 ,则
,则