题目内容
已知| |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,则
的夹角为60°,则 +
+ 在
在 方向上的投影为________.
方向上的投影为________.
2
分析:根据| |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,算出|
的夹角为60°,算出| +
+ |=
|= 且(
且( +
+ )•
)• =2.再设
=2.再设 +
+ 与
与 的夹角为θ,结合数量积公式和向量投影的定义,算出|
的夹角为θ,结合数量积公式和向量投影的定义,算出| +
+ |cosθ的值,即可得到向量
|cosθ的值,即可得到向量 +
+ 在
在 方向上的投影值.
方向上的投影值.
解答:∵| |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,
的夹角为60°,
∴ •
• =
= |×|
|×| |×cos60°=1
|×cos60°=1
由此可得( +
+ )2=|
)2=| |2+2
|2+2 •
• +|
+| |2=1+2+4=7
|2=1+2+4=7
∴| +
+ |=
|= .设
.设 +
+ 与
与 的夹角为θ,则
的夹角为θ,则
∵( +
+ )•
)• =|
=| |2+
|2+ •
• =2
=2
∴cosθ=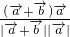 =
=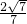 ,
,
可得向量 +
+ 在
在 方向上的投影为|
方向上的投影为| +
+ |cosθ=
|cosθ= ×
×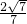 =2
=2
故答案为:2
点评:本题给出向量| |、|
|、| |和
|和 与
与 的夹角,求向量
的夹角,求向量 +
+ 在
在 方向上的投影.着重考查了向量数量积的定义、向量的夹角公式和向量投影的概念等知识,属于基础题.
方向上的投影.着重考查了向量数量积的定义、向量的夹角公式和向量投影的概念等知识,属于基础题.
分析:根据|
 |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,算出|
的夹角为60°,算出| +
+ |=
|= 且(
且( +
+ )•
)• =2.再设
=2.再设 +
+ 与
与 的夹角为θ,结合数量积公式和向量投影的定义,算出|
的夹角为θ,结合数量积公式和向量投影的定义,算出| +
+ |cosθ的值,即可得到向量
|cosθ的值,即可得到向量 +
+ 在
在 方向上的投影值.
方向上的投影值.解答:∵|
 |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为60°,
的夹角为60°,∴
 •
• =
= |×|
|×| |×cos60°=1
|×cos60°=1由此可得(
 +
+ )2=|
)2=| |2+2
|2+2 •
• +|
+| |2=1+2+4=7
|2=1+2+4=7∴|
 +
+ |=
|= .设
.设 +
+ 与
与 的夹角为θ,则
的夹角为θ,则∵(
 +
+ )•
)• =|
=| |2+
|2+ •
• =2
=2∴cosθ=
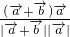 =
=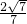 ,
,可得向量
 +
+ 在
在 方向上的投影为|
方向上的投影为| +
+ |cosθ=
|cosθ= ×
×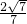 =2
=2故答案为:2
点评:本题给出向量|
 |、|
|、| |和
|和 与
与 的夹角,求向量
的夹角,求向量 +
+ 在
在 方向上的投影.着重考查了向量数量积的定义、向量的夹角公式和向量投影的概念等知识,属于基础题.
方向上的投影.着重考查了向量数量积的定义、向量的夹角公式和向量投影的概念等知识,属于基础题. 
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知
(xcosx+3a-b)dx=2a+6,f(t)=
(x3+ax+5a-b)dx为偶函数,则a+b=( )
| ∫ | 1 -1 |
| ∫ | t 0 |
| A、-6 | B、-12 | C、4 | D、-4 |