题目内容
已知等差数列{an}(n∈N+)中,an+1>an,a2a9=232,a4+a7=37,
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若将数列{an}的项重新组合,得到新数列{bn},具体方法如下:b1=a1,b2=a2+a3,b3=a4+a5+a6+a7,b4=a8+a9+a10+…+a15,…,依此类推,第n项bn由相应的{an}中2n-1项的和组成,求数列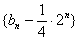 的前n项和Tn。
的前n项和Tn。
解:(Ⅰ)由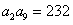 与
与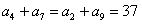 ,
,
解得: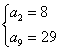 或
或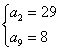 (由于
(由于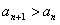 ,舍去),
,舍去),
设公差为d,
则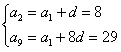 ,解得
,解得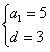 ,
,
所以数列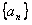 的通项公式为
的通项公式为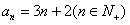 。
。
(Ⅱ)由题意得:
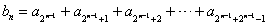
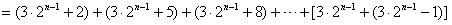
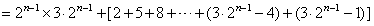 ,
,
而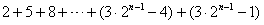 是首项为2,
是首项为2,
公差为3的等差数列的前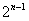 项的和,
项的和,
所以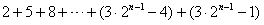
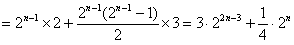 ,
,
所以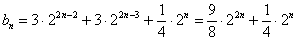 ,
,
所以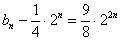 ,
,
所以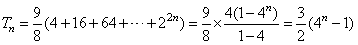 。
。
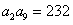 与
与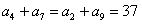 ,
,解得:
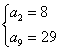 或
或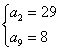 (由于
(由于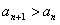 ,舍去),
,舍去),设公差为d,
则
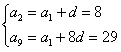 ,解得
,解得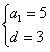 ,
,所以数列
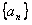 的通项公式为
的通项公式为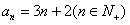 。
。(Ⅱ)由题意得:
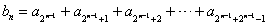
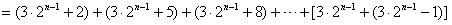
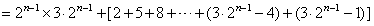 ,
,而
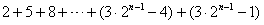 是首项为2,
是首项为2,公差为3的等差数列的前
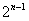 项的和,
项的和,所以
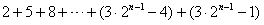
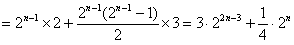 ,
,所以
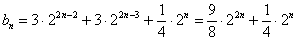 ,
,所以
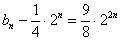 ,
,所以
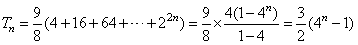 。
。
练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.