题目内容
(本题满分12分)设椭圆 ,其相应焦点
,其相应焦点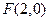 的准线方程为
的准线方程为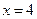 .
.
(1)求椭圆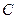 的方程;
的方程;
(2)过点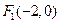 作两条互相垂直的直线分别交椭圆
作两条互相垂直的直线分别交椭圆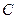 于点
于点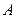 、
、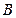 和
和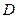 、
、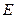 ,
,
求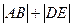 的最小值.
的最小值.
 ,其相应焦点
,其相应焦点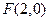 的准线方程为
的准线方程为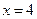 .
.(1)求椭圆
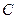 的方程;
的方程;(2)过点
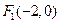 作两条互相垂直的直线分别交椭圆
作两条互相垂直的直线分别交椭圆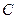 于点
于点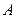 、
、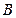 和
和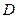 、
、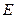 ,
,求
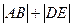 的最小值.
的最小值. (1)椭圆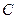 的方程为
的方程为
(2)当 时,
时,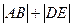 取得最小值
取得最小值
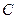 的方程为
的方程为
(2)当
 时,
时,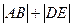 取得最小值
取得最小值
解:⑴由题意得:  ,
, 椭圆
椭圆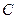 的方程为
的方程为
(2)设直线 的倾斜角为
的倾斜角为 ,由(1)知
,由(1)知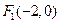 是椭圆
是椭圆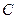 的左焦点,离心率
的左焦点,离心率 ,
,
椭圆的左准线 ,作
,作 ,
, 与
与 轴交于点H(如图) ,
轴交于点H(如图) ,
 点A在椭圆上,
点A在椭圆上,



 , 同理
, 同理  ,
,
 。
。
即 ,
,
由于 所以
所以 ,
,

当 时,
时,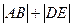 取得最小值
取得最小值
 ,
, 椭圆
椭圆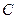 的方程为
的方程为
(2)设直线
 的倾斜角为
的倾斜角为 ,由(1)知
,由(1)知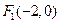 是椭圆
是椭圆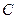 的左焦点,离心率
的左焦点,离心率 ,
,椭圆的左准线
 ,作
,作 ,
, 与
与 轴交于点H(如图) ,
轴交于点H(如图) , 点A在椭圆上,
点A在椭圆上,



 , 同理
, 同理  ,
, 。
。即
 ,
,由于
 所以
所以 ,
,
当
 时,
时,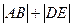 取得最小值
取得最小值

练习册系列答案
相关题目
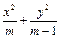 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及 直线
直线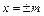 的交点从左到右的顺序为A、B、C、D,设
的交点从左到右的顺序为A、B、C、D,设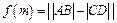 .
.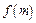 的解析式;
的解析式;
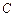 :
: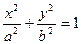 (a>b>0)的中心在原点,焦点在
(a>b>0)的中心在原点,焦点在 轴上,离心率为
轴上,离心率为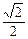 ,点F1、F2分别是椭圆的左、右焦点,在直线x=2上的点P(2,
,点F1、F2分别是椭圆的左、右焦点,在直线x=2上的点P(2, 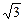 )满足|PF2|=|F1F2|,直线l:y=kx+m与椭圆C交于不同的两点A、 B.
)满足|PF2|=|F1F2|,直线l:y=kx+m与椭圆C交于不同的两点A、 B.
 存在点Q,满足
存在点Q,满足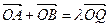 (O为坐标原点),求实数l的取值范围.
(O为坐标原点),求实数l的取值范围.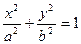 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P 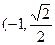 )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。 是椭圆上异于长轴端点的任一点,对于△ABC,求
是椭圆上异于长轴端点的任一点,对于△ABC,求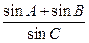 的值。
的值。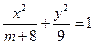 的离心率是
的离心率是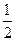 ,求椭圆两准线间的距离。
,求椭圆两准线间的距离。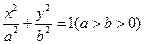 的离心率为
的离心率为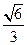 ,过
,过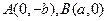 的直线与原点的距离为
的直线与原点的距离为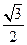
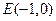 ,直线
,直线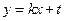 与椭圆交于不同两点C,D,试问:对任意的
与椭圆交于不同两点C,D,试问:对任意的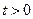 ,是否都存在实数
,是否都存在实数 ,使得以线段CD为直径的圆过点E?证明你的结论
,使得以线段CD为直径的圆过点E?证明你的结论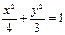 (B)
(B)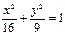 (C)
(C)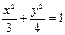 (D)
(D)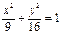
 为短轴一端点,若
为短轴一端点,若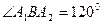 ,则椭圆的离心率为( )
,则椭圆的离心率为( )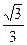
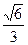
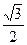
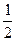
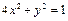 及直线
及直线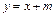 ,当直线被椭圆截得的弦最长时的直线方程为
,当直线被椭圆截得的弦最长时的直线方程为